使用初中知识理解什么是AI大模型

现在最火的科技主题就是人工智能（Artificial Intelligence，AI），所以，在各种媒体和平时交谈时，总能听到或者看到“大模型”、“参数”、“训练”等等这些概念。那么，什么是AI里的“模型”呢？

| 初中知识回顾

如果你认为自己是学渣，担心看不懂这篇文章，没关系，我们先来回顾一下初中知识。如果有两个变量：x 和 y，它们之间的关系可以表示成下面的形式：

那么，我们就说 y 是 x 的一次函数，x 是自变量。假设有一个一次函数，它是这样的：y = 3x + 5，它表示两个数之间这样的一种关系：其中一个数放大3倍后，仍然比另一个数少5；或者说，其中一个数放大3倍后，再加上5，就等于另一个数。那么，1和8就满足这种关系，2和11也满足这样的关系，依此类推。如果将这个函数放在平面直角坐标系，它的图像是这样的一条直线：

在一次函数中，k 表示这条直线的倾斜程度，我们称之为斜率；b 表示这条直线与 y 轴的交点纵坐标，我们称之为截距。也就是说，在知道了 k 和 b 的取值，以及 x 和 y 之间的这种对应关系的前提下，只要我们给定一个 x 的值（输入），我们一定能够得到一个结果值（输出）。

如果阅读到这里，你还没有放弃的话，恭喜你，你已经打败了90%的人。

| 计算机工作的基本逻辑

其实，在这里我们并不能真正地将计算机的工作原理抽丝剥茧地讲清楚，那估计把我这个公众号写爆都写不完。我们只需要知道它运作的基本逻辑就行了，这个逻辑非常简单：计算机是根据我们预先设置好的计算逻辑来执行它的计算任务的，在这个计算逻辑已知的前提下，我们告诉计算机所需处理和计算的数据，计算机就会一步步地按照我们指定的计算逻辑进行计算，最后把计算结果反馈给我们，比如：

你可以这样理解“计算逻辑”的概念：它其实就是一个输入数据与输出数据之间的对应关系，就像 y = 3x + 5 这个一次函数那样，它能对输入数据进行计算，然后给出计算结果，在计算机中，我们称这样的“计算逻辑”为程序。

如果阅读到这里，你还没有放弃的话，恭喜你，你已经打败了95%的人。

| 如果没有计算逻辑怎么办？

这时候你会发现，如果希望计算机帮我们工作，我们需要先告诉计算机这个计算逻辑是什么，或者说要先告诉计算机，我们希望进行什么样的计算，这样计算机才能开始工作。但是有的时候，我们其实无法告诉计算机，这个计算逻辑是什么，我们只有一堆来自现实世界的已知数据，我们希望计算机根据这些已知数据，找到其中的规律，然后当我们再一次将输入数据提供给计算机后，它能够根据这种规律给出最终答案。

比如天气预测，假设我们知道第二天的天气一定是跟前一天的气温和风速有关，当然如果我们知道这个关系具体是什么，那么我们就可以设定这个计算逻辑，让计算机根据前一天的气温和风速来计算第二天的天气，天气预报也就变得特别简单了。可惜的是，我们并不知道这个关系（计算逻辑）是什么，这时候，我们就会将过去几十年的天气数据发送给计算机，让它从中找出规律，并总结出这套计算逻辑。这样的话，今后我们只需要将今天的气温和风速告诉计算机，它就能帮忙预测明天的天气了。

当然，让计算机“找出规律”这件事，也不是一件容易的事，这个过程是需要基于大量的数据的，而且还需要采用科学的方法来完成。说得更专业一点，“找出规律”的过程，就是训练的过程，在这个过程中所选择的“科学方法”，称之为拟合方法。

如果阅读到这里，你还没有放弃的话，恭喜你，你已经打败了97%的人。

| 拟合方法：线性拟合举例

这里我们用最简单的拟合方法：线性拟合举例。所谓之线性拟合，就是指找出两个数值之间的线性关系，也就是找出一个 y = kx + b 的一次函数，它可以表示两个数值之间的关系。假设我们有6个数据（每个数据包含输入x和输出y的值）：

(0, 8)	(1, 8)	(2, 14)
(3, 11)	(4, 17)	(5, 20)

如果将这6个数据标在平面直角坐标系中，可以看到，根据这6个点的分布，我们大致可以找到一条直线，使得这些点到这条直线的平均距离最短：

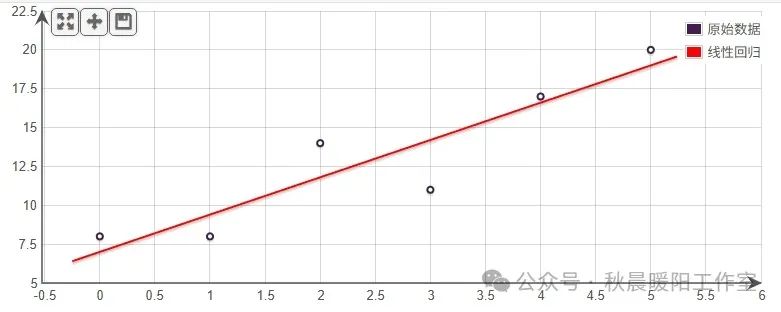
此时，这根直线的方程式为：y = 2.4x + 7。当然，这是基于6个数据的拟合结果。到这里，你已经可以拿这个函数，来预测当 x = 20 的时候，结果会是什么（这里结果为55）。不过，由于我们的数据量太小，这个线性拟合不一定精确。为了提高精确度，我们需要使用更多的数据。

现在，我们提供12个数据（在原来的基础上，增加6个）：

(0, 8)	(1, 8)	(2, 14)
(3, 11)	(4, 17)	(5, 20)
(6, 22)	(7, 28)	(8, 30)
(9, 31)	(10, 34)	(11, 36)

此时，这些点在平面直角坐标系中的分布和拟合直线如下：

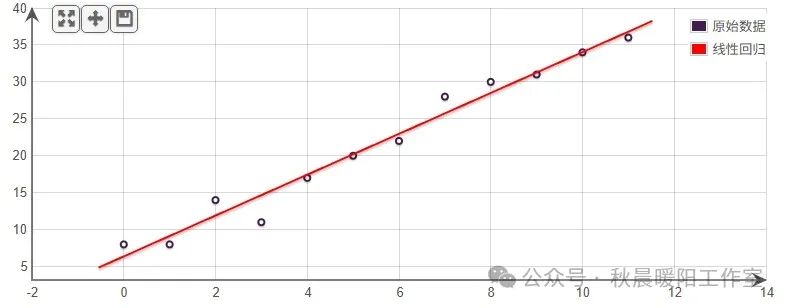
这根直线的方程为：y = 2.76573x + 6.37179。如果拿这个函数来再次预测当 x= 20 的时候，结果会是什么，我们可以得到，当 x = 20 时，计算结果为61.68639。

或许12个数据仍然不是那么的精确，我们再多加一些数据，看看效果如何。现在，我们使用30个数据进行线性拟合（在原来的基础上，增加18个）：

(0, 8)	(1, 8)	(2, 14)
(3, 11)	(4, 17)	(5, 20)
(6, 22)	(7, 28)	(8, 30)
(9, 31)	(10, 34)	(11, 36)
(12, 38)	(13, 41)	(14, 45)
(15, 50)	(16, 49)	(17, 57)
(18, 56)	(19, 60)	(20, 65)
(21, 69)	(22, 68)	(23, 73)
(24, 75)	(25, 79)	(26, 84)
(27, 87)	(28, 89)	(29, 92)

这次，这些点在平面直角坐标系中的分布和拟合直线如下：

这根直线的方程为：y = 2.96329x + 4.89892。如果拿这个函数来再次预测当 x= 20 的时候，结果会是什么，我们可以得到，当 x = 20 时，计算结果为64.16472。

你有没有发现什么规律？三次线性拟合，我们提供的样本数据量从少到多，我们得到了三个不同的线性函数，用同样的输入值20来计算输出值，分别得到三个结果：55、61.68639 和 64.16472。而从我们的这些样本数据中，我们已经知道了，实际上如果输入20的话，应该得到65（上表中的蓝色数据），这样看来，第三次拟合所得到的一次函数最贴近实际。因此，我们得到了这个结论：样本数据量越多，拟合方法就越能接近实际，用拟合方法所得到的函数去做预测就会越准确。

当然，在实际中，所使用的拟合方法会复杂很多，这里只是为了将问题说明白，所以才选择了线性拟合这一最简单的拟合方法。

如果阅读到这里，你还没有放弃的话，恭喜你，你已经打败了99%的人，因为，你已经成功地训练出了一个AI模型，并能用它来进行预测。

| 什么是AI大模型？

回到我们刚才通过线性拟合得到的一次函数：y = 2.96329x + 4.89892，它就是AI模型。2.96329 和 4.89892 是模型的两个参数，获得 y 和 x 的基于这两个参数的关系（y 是等于 x 乘以 2.96329 之后，再加上 4.89892 所得到的结果，而不是等于 x 加上 4.89892 再乘以 2.96329的结果）的过程，就是拟合方法。通过各种不同的拟合方法和大量的数据，最终确定了可以用于计算和推断的函数（数学公式，也就是模型）的过程，称之为模型训练。

那什么是大模型呢？在上面的例子中，我们的模型 y = 2.96329x + 4.89892 只包含两个参数，而在实际中，由于不同的模型解决的实际问题不同，模型包含的参数个数会相当多，你经常会看到像2.3B、7B、14B这样的单位，B是Billion的意思（10亿），2.3B就是23亿，也就是这个模型包含了23亿个参数。DeepSeek满血版参数个数为671B，也就是6710亿，你说大不大？（大！！）参数大，数据量就大，对应的模型文件也很大，运行起来所需的计算和存储资源也会更多。所以，“大”字名副其实！

| 总结

通过给定输入数据和计算逻辑，获得结果输出，这个过程就是传统的计算机运算；通过输入和结果数据，推导计算逻辑，这个过程就是模型训练，推导出来的计算逻辑就是AI模型。如果阅读到这里，你还没有放弃的话，恭喜你，你已经理解什么是AI大模型了！

| 引用

本文中拟合线的绘制与拟合函数的生成，使用了“紫竹叽歪”提供的在线工具，地址：https://zizhujy.js.org/