数论 --- 筛素数

筛素数

如何求出从 $1\sim n$ 中素数的个数

---

方法 $1$ 暴力枚举 ------ $O(n^2)$
从 $1\sim n$ 遍历一遍，每一个数都去判断一下，这个数是否是素数，如果是 $ans=ans+1$ 。时间复杂度 $O(n\ast n^{1/2})$ 。

void get_primes(int n)
{
    int ans = 0;
    for (int i = 2; i <= n; i ++)
    {
        int f = 0;
        //判断是否是质数
        for (int j = 2; j <= i / j; j++)
        {
            if(i % j == 0)
            {
                f = 1;
                break;
            }
        }
        if(f == 0)ans++;//是质数的话ans++
    }
    printf("%d\n",ans);
}

很明显 $O(n^2)$ 级别的复杂度，在一般的算法题中，只要 $n$ 超过 $1e5$ 基本上就要超时了，而且暴力枚举也不符合我们所谓筛素数的标题，那么怎么样才能叫做筛素数呢？

---

方法 $2$ 朴素筛法 ------ $O(n\ast log(n))$

• 既然是筛法，那到底如何来筛呢？筛什么呢？
  显然，我们要筛的是素数，也就是在 $2\sim n$ 这么一个数表中，把合数全部去掉，那么留下来的或者说是我们筛出来的也就是我们要的素数了。

举个例子 当 $n=25$ 时，我们先把从 $1$ ~ $25$写在一个数表中

次数/数字	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
第零次	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
第一次：筛 2 的倍数	Y	—	N	—	N	—	N	—	N	—	N	—	N	—	N	—	N	—	N	—	N	—	N	—
第二次：筛 3 的倍数	Y	Y	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	—
第三次：筛 4 的倍数	Y	Y	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	—
第四次：筛 5 的倍数	Y	Y	N	Y	N	—	N	N	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	N
第五次：筛 6 的倍数	Y	Y	N	Y	N	—	N	N	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	N
第六次：筛 7 的倍数	Y	Y	N	Y	N	Y	N	N	N	—	N	—	N	N	N	—	N	—	N	N	N	—	N	N

我们可以发现：

第一次筛的时候，把 $1$ ~ $n$ 中 $2$ 的倍数全部筛去
第二次筛的时候，把 $1$ ~ $n$ 中 $3$ 的倍数全部筛去
第三次筛的时候，把 $1$ ~ $n$ 中 $4$ 的倍数全部筛去
第四次筛的时候，把 $1$ ~ $n$ 中 $5$ 的倍数全部筛去
$\cdot$
$\cdot$
$\cdot$
第二十四次筛的时候，把 $1$ ~ $n$ 中 $25$ 的倍数全部筛去

我们可以发现，当轮到某个数 $k$ 开始筛它的倍数的时候，同时 $k$ 没有被前面的数筛掉，那么 $k$ 就是一个质数，因为在 $2$ ~ $k-1$ 中没有 $k$ 的因子。

下图形象的体现我们筛质数的思想

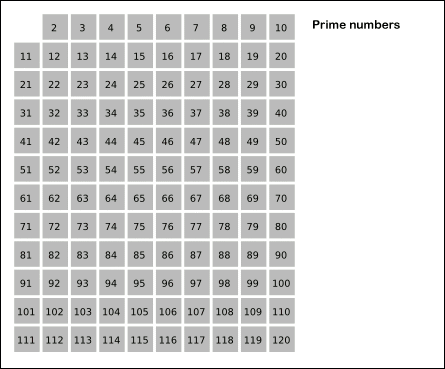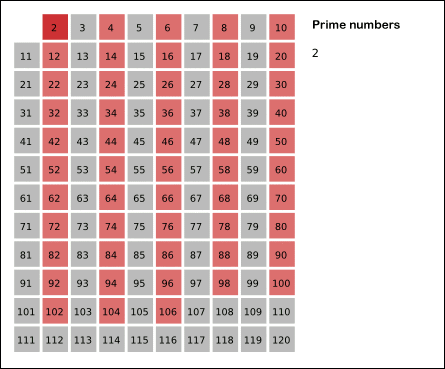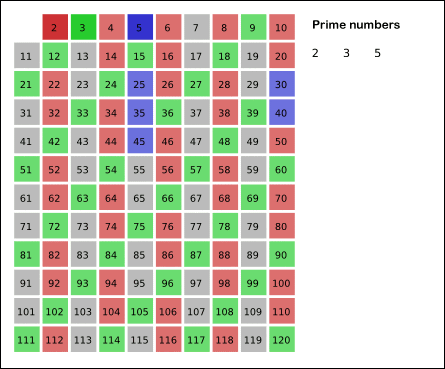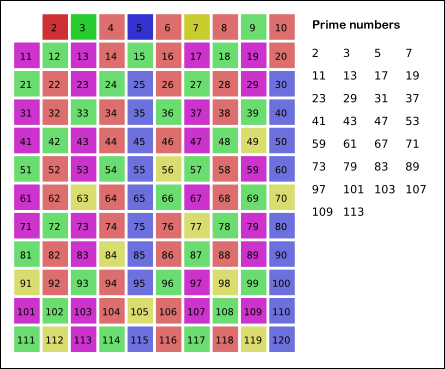
（动图出处： https://www.cnblogs.com/findwg/p/4901219.html）

接下来请看普通筛法的代码。

const int N = 1e6+10;
int primes[N];//用来存放素数
bool st[N];//用来判断某个数是否是素数 false 表示是质数  true 表示不是质数
void get_primes(int n)
{
    int cnt = 0;//统计质数的个数
    st[1] = true;//1 不是 质数
    for (int i = 2; i <= n; i ++)
    {
        if(!st[i])primes[cnt++] = i;//如果轮到这个数开始筛了，并且这个数还没有被筛掉，那么这个数就是质数，把它放到primes里去
        for (int j = i + i; j <= n; j += i)st[j] = true;//遍历一遍 i 的倍数，把它们都筛掉
    }
    int ans = 0;
    for (int i = 1; i <= n; i ++)//遍历一遍 1 ~ n 如果是素数，ans++
        ans += !st[i];
    printf("%d\n", ans);    
}

我们可以简单的来算一下按照朴素筛法来筛素数的一个时间复杂度。对于 $n$ 来说，第一次筛 $\frac{n}{2}$ 个数，第二次筛 $\frac{n}{3}$ 个数 ··· 第 $n$ 次筛 $\frac{n}{n-1}$ 个数。
那么总的时间是 $\frac{n}{2}+\frac{n}{3}+\cdot \cdot \cdot +\frac{n}{n-1}$ ,这就等于$n\ast (\frac{1}{2}+\frac{1}{3}+\cdot \cdot \cdot +\frac{1}{n-1})$ ，那么这就是一个调和级数。当 $\underset{n\to \infty }{\lim }$时 调和级数的值大概为 $ln(n)+c(欧拉常数，c\approx 0.577)$ (可直接拿来用的，详细证明可以看百度百科) 。
那么普通筛法的时间复杂度大概为 $O(n\ast ln(n))$ , $ln(n)<lo{g}_2(n)$ ，所以 $n=1e9$ 的时候 $ln(n)\approx 32$，比起我们第一种筛法的$\sqrt{n}\approx 4e4\sim 5e4$ 要快得多。

---

方法 $3$ 埃氏筛 ------ $O(n\ast log(log(n)))$

埃拉托斯特尼筛法，简称埃氏筛。

埃氏筛的核心思想就是筛去 $1\sim n$ 中所有质数的倍数。

埃氏筛与朴素筛法相比较，就是加了一个限制条件，我们在筛的时候，只需要筛所有素数的倍数即可。

举个简单的例子，轮到 $2$ 筛的时候，它会把后面所有因子中 $2$ 的数全部筛完，它会把$4，6，8，10，12\cdot \cdot \cdot n$全部筛掉，而当轮到 $4$ 筛的时候，它又会筛到$8，12$ 。 很明显这一部分是重复计算的，所以埃氏筛的核心思想，就是去掉这重复筛的部分，只需要从所有的质数开始筛即可。

而之前说了，如果轮到当前这个数开始筛，并且当前这个数还没被筛过，那这个数就是个质数。

接下来这个是埃氏筛的代码

const int N = 1e6+10;

int primes[N];
bool st[N];
void get_primes(int n)
{
    int cnt = 0;
    st[1] = true;
    for (int i = 2; i <= n; i ++)
    {
        if(!st[i])
        {
            primes[cnt++] = i;
            for (int j = i + i; j <= n; j += i)st[j] = true;
            //唯一改动的地方，把for循环筛合数，放到了if条件中，如果 i 是素数，才去往后筛合数
        }
    }
}

然后我们再来看一下埃氏筛的时间复杂度。
我们从需要算 $(\frac{1}{2}+\frac{1}{3}+\cdot \cdot \cdot +\frac{1}{n-1})$ 这个调和级数减少到了，只需要算这之中所有质数的调和级数即可。
根据质数定理可知 $1\sim n$ 之中大概有 $\frac{n}{ln(n)}$ 个质数

所以本来我们需要算 $n$ 个数的调和级数，现在只需要算 $\frac{n}{ln(n)}$ 个数的调和级数，所以时间复杂度大概在 $O(n\ast ln(n)/ln(n))$ 。但是这不等于它是一个 $O(n)$ 的算法，因为其中的复杂度不能这样简单的计算，而埃氏筛的时间复杂度大概是 $O(n\ast log(log(n)))$ 级别，举个例子，当$n=2^{32}$时，$log(log(n)))=5$ 。

ps:关于质数基本定理，这是某数学家证明的定理，具体步骤极其复杂，详细证明请百度百科

---

方法 $4$ 线性筛 （欧拉筛） ------ $O(n)$

接下来我们要讲的一个筛法叫做线性筛，或者也叫欧拉筛。
根据上面的归纳，其实我们不难发现，为什么埃氏筛它不能算是线性的或者说是 $O(n)$ 的复杂度。

因为很明显，即使是你只筛去所有质数的倍数，那也会有很多数被你重复筛掉，比如 $6$ 同时被 $2$ 和 $3$ 筛了两次，$10$ 同时被 $2$ 和 $5$ 筛了两次，$30$ 同时被 $2，3，5$ 筛了三次，所以你仍旧有合数被筛去不止一次。

那么我们是否有办法让每个合数只被筛去一次呢？如果可以的话，那这样的筛法就是完全的线性了。当然，这是存在的。

根据唯一分解定理(传送门)可知，一个数可以被唯一地分解为若干个质数的乘积。
那么我们规定，每次在筛一个合数的时候，只用它最小的素因子去筛掉它，这样就能保证了，每个数只被筛一次。
思路就是这么简单，那么我们看看代码怎么去写。

const int N = 1e6+10;
int primes[N];
bool st[N];
void get_primes(int n)
{
    int cnt = 0;
    st[1] = true;
    for (int i = 2; i <= n; i ++)
    {
        //------>
        if(!st[i])primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j ++)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0)break;
        }
        //<------
    }  
}

我们可以看到其实改动的地方就只有箭头里面的内容，那么我们现在来分析，为什么这样就可以让每个合数都被它最小的质因子筛掉呢？
首先，我们知道 $primes[j]$ （之后简称$p_j$）表示的是所有质数的一个集合。
我们分两种情况来考虑

1. $i\%p_j=0$ 因为 $j$ 是从 $0$ 开始枚举，也就是说 $p_j$ 一定是 $i$ 的最小的质因子，又因为 $p_j$ 本身是一个质数，或者说 $p_j$ 一定也是 $p_j$ 的最小的质因子，那么 $p_j$ 一定是 $p_j\ast i$ 的最小质因子。（此时我们就用 $p_j$ 把 $p_j\ast i$ 筛掉了）

2. $i\%p_j\ne 0$ 同样因为 $j$ 是从 $0$ 开始枚举，又因为 $i\%p_j\ne 0$ ，也就是说 $p_j$ 一定比 $i$ 的最小的质因子还要小，而 $p_j$ 本身是一个质数，那么 $p_j$ 也一定是 $p_j\ast i$ 的最小质因子。（此时我们也实现了用 $p_j\ast i$ 的最小质因子 $p_j$ ，把 $p_j\ast i$ 筛掉了）

注意：我们每次筛的都是 $primes[j]\ast i$ 这个数。

这就是欧拉筛的核心思想，可能会有点绕，这两种情况需要大家多读几遍，多体会一下。

接下来，我们再来分析 $if(i\%primes[j]==0)break;$

很显然，因为我们希望用合数的最小质因子去筛所有的合数，为了确保 $p_j$始终是 $p_j\ast i$ 的最小质因子，当 $i\%p_j=0$ 时，我们就不希望再去筛 $i\ast p_{j+1}$，因为这样 $i\ast p_{j+1}$ 的最小质因子就一定不是$p_{j+1}$ ，很显然 $p_j$ 是 $i$ 的质因子，而 $p_{j+1}>p_j$，所以这样就会使得一个合数被反复筛去，而并没有达到我们所说的：每个合数只被它的最小质因子筛去。

然后我们再来分析这个$for$循环 $for(intj=0;primes[j]<=n/i;j++)$

$for$循环从$0$开始枚举 $primes$ 数组中现有的所有的质数，因为我们是要筛的质数是 $p_j\ast i$ 所以 $p_j\ast i\le n$，同样为了避免 $p_j\ast i$ 溢出，所以我们写成 $primes[j]<=n/i$ 。

这里有的同学说 从$0$开始枚举 $primes$ 数组中现有的所有的质数，需不需要加限制条件 $j<cnt$ 。

答案是： $j<cnt$ 没必要，因为你会发现 $primes[cnt-1]=$ 当前最大质数
如果 $i$ 不是质数，根据唯一分解定理，$i$ 可以被唯一地分解为若干个质数的乘积，那么当枚举 $p_j$ 为 $i$ 的最小质因数时，就会被 $break$ 掉。
如果 $i$ 是质数，那么 $primes[cnt-1]=i$，当 $j$ 枚举到 $cnt-1$时，循环也会跳出。

---

我们可以来看一下这个程序大致是怎样运行的

我们可以看到所有的合数，的的确确只被筛过一次。

---

最后我们再来简单地分析一下欧拉筛的时间复杂度，虽然看着是两层循环，但实际上，我们对于每个数只会通过它最小的质因子将它筛去，所以本质上只是将每个数都跑了一遍，所以它的时间复杂度就是$O(n)$ 。我们可以拿欧拉筛与埃氏筛进行比较一下，当$n=1e9$ 时，欧拉筛大概比埃氏筛快 $5$ 倍，当$n=1e7$时，欧拉筛大概比埃氏筛快 $2\sim 3$ 倍。

最后，欧拉筛基本上算是数论中最简单的算法，希望同学们能够继续加油，我也继续加油（doge）。