本文介绍了一种密钥封装与加解密的方法，包括密钥的封装与解封过程，以及加密与解密的具体步骤。文章详细阐述了密钥封装原理，并通过实例说明了如何使用该技术实现信息安全传输。
A.4 第4部分——密钥封装和加解密
A.4.1 密钥封装（User A）
K是用户A的生成密钥，C是封装信息，用于对方解封得到相同的密钥K。
A.4.2 密钥解封（User B）
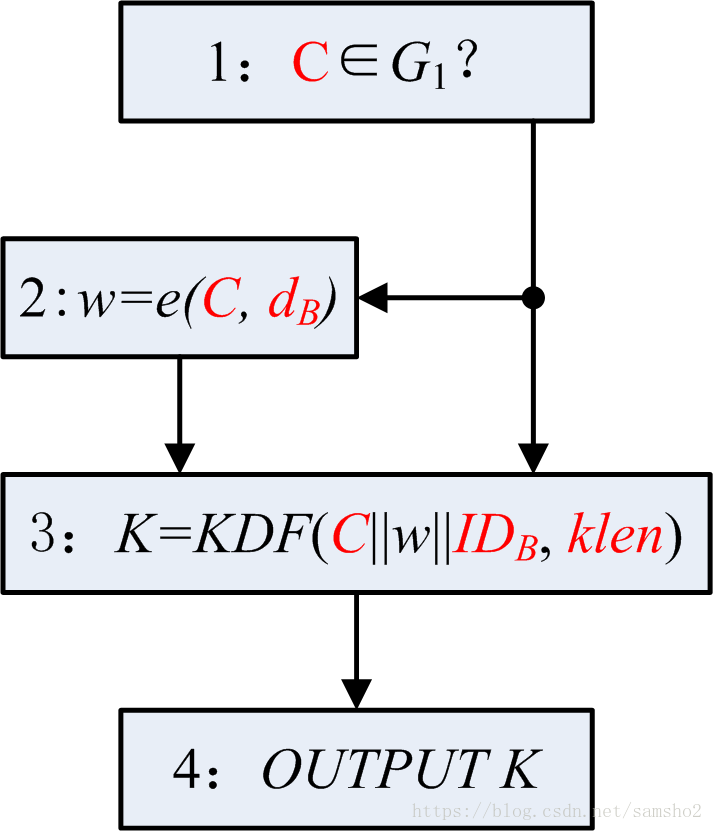
A.4.3 密钥封装原理
从以上推导可知，双方计算出来的w相等，C是一样的，所以KDF计算值相等
A.4.4 加密（User A）
|
| 流加密 | 分组加密 |
| klen | k1长度+k2长度 | k1长度+k2长度 |
| k1长度 | M长度 | 对称密码算法的密钥长度 |
| k2长度 | 未定义，测试向量中为256 | 未定义，测试向量中为256 |
| C2 | C2=K1⊕M | C2=Enc(K1, M) |
A.4.5 解密（User B）
|
| 流加密 | 分组加密 |
| klen | k1长度+k2长度 | k1长度+k2长度 |
| k1长度 | C2长度 | 对称密码算法的密钥长度 |
| k2长度 | 未定义，测试向量中为256 | 未定义，测试向量中为256 |
| C2 | M =K1⊕C2 | M=Enc(K1, C2) |
A.4.6 加解密原理
同密钥封装原理
扫一扫
3730
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
