POJ 2991 Crane 线段树

这个题比较神奇。大意就是有一个长杆，杆上有一些关节点，可以转动，然后每次操作就是将某个关节点的角度变成某个角度，最后求末尾的坐标。

线段树每个结点存的信息是，这一段末尾的x坐标，y坐标，以及该段与y轴的夹角，其中x,y坐标是与上一段线段的相对坐标。这样的好处是显而易见的。注意，这个与y轴的夹角是该段线段顺时针旋转至初始状态的角度，如下图

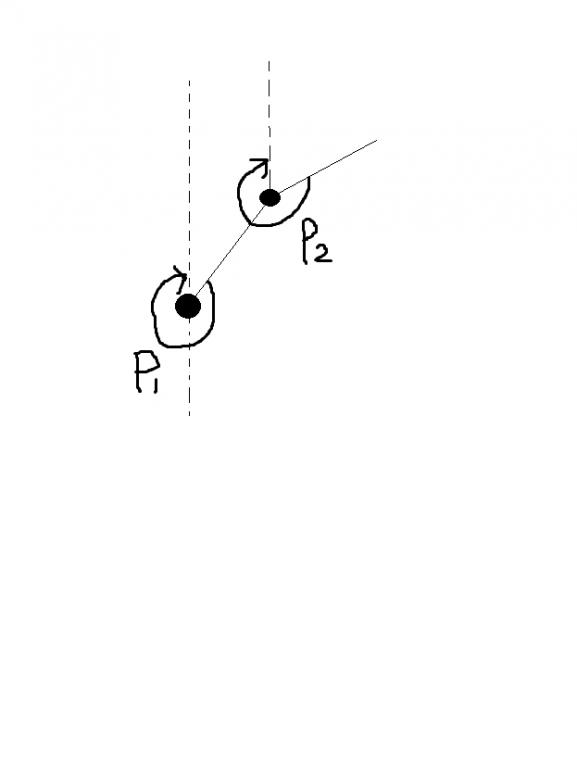
然后每次更新的时候需要注意，是把某个结点后的所有线段都旋转

/*
ID: sdj22251
PROG: inflate
LANG: C++
*/
#include <iostream>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <queue>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#define MAXN 10005
#define INF 1000000000
#define L(x) x<<1
#define R(x) x<<1|1
#define PI acos(-1.0)
#define eps 1e-7
using namespace std;
int len[MAXN];
struct node
{
    int left, right, mid;
    double x, y;
    int turn;
}tree[4 * MAXN];
void up(int C)
{
    tree[C].y = tree[L(C)].y + tree[R(C)].y;
    tree[C].x = tree[L(C)].x + tree[R(C)].x;
}
void change(int C, int turn)
{
    tree[C].turn = (tree[C].turn + turn) % 360;
    double tx = tree[C].x;
    double ty = tree[C].y;
    double degree = turn * 1.0 / 180.0 * PI;
    tree[C].x = tx * cos(degree) - ty * sin(degree);
    tree[C].y = tx * sin(degree) + ty * cos(degree);
}
void down(int C)
{
    if(tree[C].turn)
    {
        change(L(C), tree[C].turn);
        change(R(C), tree[C].turn);
        tree[C].turn = 0;
    }
}
void make_tree(int s, int e, int C)
{
    tree[C].left = s;
    tree[C].right = e;
    tree[C].mid = (s + e) >> 1;
    tree[C].x = 0;
    tree[C].turn = 0;
    if(s == e) {tree[C].y = len[s]; return;}
    make_tree(s, tree[C].mid, L(C));
    make_tree(tree[C].mid + 1, e, R(C));
    up(C);
}
int query(int C, int p)
{
    if(tree[C].left == tree[C].right)
        return tree[C].turn;
    down(C);
    if(tree[C].mid >= p) return query(L(C), p);
    else return query(R(C), p);
}
void update(int s, int e, int turn, int C)
{
    if(tree[C].left >= s && tree[C].right <= e)
    {
        change(C, turn);
        return;
    }
    down(C);
    if(tree[C].mid >= s) update(s, e, turn, L(C));
    if(tree[C].mid < e) update(s, e, turn, R(C));
    up(C);
}
int main()
{
    int n, c;
    int x, y;
    bool fg = 0;
    while(scanf("%d%d", &n, &c) != EOF)
    {
        if(fg) puts("");
        fg = 1;
        for(int i = 1; i <= n; i++)
            scanf("%d", &len[i]);
        make_tree(1, n, 1);
        for(int i = 1; i <= c; i++)
        {
            scanf("%d%d", &x, &y);
            int pos1 = query(1, x);
            int pos2 = query(1, x + 1);
            int t = (-180 + pos1 - pos2 + y + 360) % 360;
            update(x + 1, n, t, 1);
            printf("%.2f %.2f\n", tree[1].x + eps, tree[1].y + eps);
        }
    }
    return 0;
}