编程之美--3.7 队列中取最大值操作问题

思路1

---

1 利用堆的原理来解决问题。

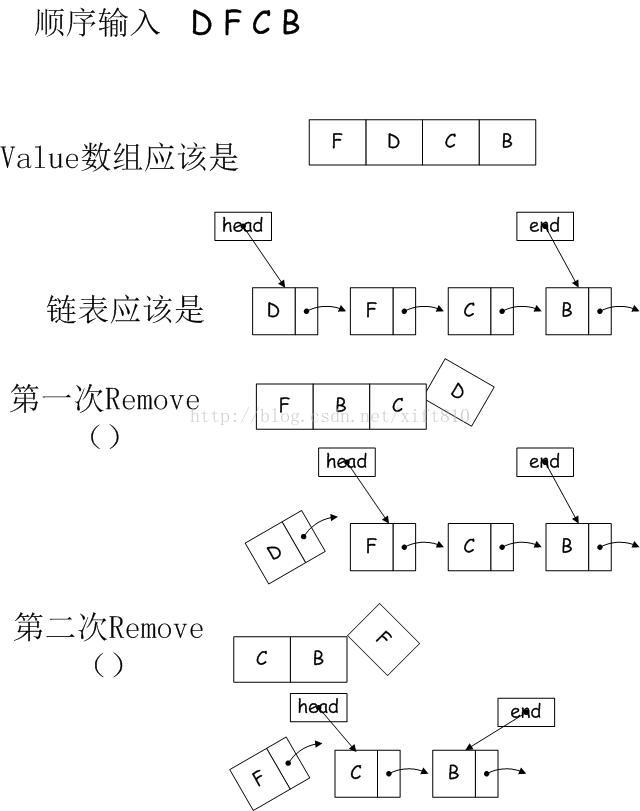
2 需要先决定使用什么样的数据结构。我的queen里有一个数组，数组是按照元素值的大小来排放的堆；还有一个链表，链表中含有的是一个Node形式。Node是自创的，包含数据值value，按顺序下一条的元素node 和 自己对应在堆中的index。

3 实现过程中有很多细节，对于领会和灵活应用堆非常有帮助。最好自己能够写一下。

4

代码1

---

class MyQueenBasicHeap{
	int heapLastIndex ;
	int maxn;
	MyNode[] heap;
	MyNode head;
	MyNode end;
	
	public MyQueenBasicHeap(int maxn){
		this.maxn = maxn;
		heapLastIndex = 0;
		heap = new MyNode[maxn];
		head = null;
		end = null;
	}
	
	public void add(char c) throws Exception{
		if(heapLastIndex==maxn){
			throw new Exception();
		}
		MyNode cur = new MyNode(c);
		if(heapLastIndex == 0){
			end =cur;
			head = cur;
		}
		else{
			end.next = cur;
			end = cur;
		}
		heapInsertKey(heapLastIndex, cur);
		heapLastIndex++;	
	}
	
	public char remove() throws Exception{
		if(heapLastIndex ==0){
			throw new Exception();
		}
		MyNode cur = head;
		head = head.next;
		heapDeleteKey(cur);
		
		return ' ';
	}
	
	public char Max() throws Exception{
		if(heapLastIndex == 0){
			throw new Exception();
		}
		return  heap[0].val;
	}
	private void heapDeleteKey(MyNode cur){
		int index = cur.index;
		swap(heap,index,heapLastIndex-1);
		heapLastIndex--;
		
		if(index>0){
			while(index>0&&heap[index].val>heap[Parent(index)].val){
				swap(heap,Parent(index),index);
				index = Parent(index);
			}
		}
		else{
			maxHeapify(index);
		}
		
		
	}
	private void maxHeapify(int index) {
		int largest;
		int left = Left(index);
		int right = Right(index);
		if(left<heapLastIndex && heap[left].val>heap[index].val){
			largest = left;
		}
		else{
			largest = index;
		}
		if(right<heapLastIndex && heap[right].val>heap[largest].val){
			largest = right;
		}
		if(largest!=index){
			swap(heap,largest,index);
			maxHeapify(largest);
		}
		
	}

	private void heapInsertKey(int i, MyNode cur){
		heap[i] = cur;
		while(i>0 && heap[Parent(i)].val<heap[i].val){
			swap(heap,Parent(i),i);
			i = Parent(i);
		}
		cur.index = i;
		
	}
	private void swap(MyNode[] heap, int i, int j) {
		MyNode temp = heap[i];
		heap[i] = heap[j];
		heap[i].index = i;
		heap[j] = temp;
		heap[j].index = j;
		
	}

	private int Parent(int i){
		return (i-1)/2;
	}
	private int Left(int i){
		return 2*i+1;
	}
	private int Right(int i){
		return 2*i+2;
	}
}

class MyNode{
	char val;
	MyNode next;
	int index;
	
	public MyNode(char val){
		this.val = val;
	}
	public MyNode(char val,MyNode next){
		this.val = val;
		this.next = next;
	}
}

思考2

---

1 用两个stack来实现queen，老题了，这个要非常熟悉。

代码2

---

class MyStack{
	//放元素的数组
	private char[] item;
	private int stacktop;
	//放最大数的指针的数组
	private int[] link2NextMaxItem;
	private int maxStackItemIndex;
	//数组最大的大小
	private int maxn ;
	
	public MyStack(int n){
		maxn = n;
		item = new char[n];
		stacktop = -1;
		link2NextMaxItem = new int[n];
		maxStackItemIndex = -1;
	}
	
	public void push(char c) throws Exception{
		stacktop++;
		if(stacktop>maxn-1){
			throw new Exception();
		}
		else{
			item[stacktop] =c;
			if(c > Max()){
				link2NextMaxItem[stacktop] = maxStackItemIndex;
				maxStackItemIndex = stacktop;
			}
			else{
				link2NextMaxItem[stacktop] =-1;
			}
		}
	
	}
	
	public char pop() throws Exception{
		if(stacktop<0){
			throw new Exception();
		}
		char ret = item[stacktop];
		if(stacktop == maxStackItemIndex){
			maxStackItemIndex = link2NextMaxItem[stacktop]	;
		}
		stacktop--;
		return ret;
	}
	
	public char Max(){
		if(maxStackItemIndex>=0){
			return item[maxStackItemIndex];
		}
		else{
			return Character.MIN_VALUE;
		}
	}
	public boolean isEmpty(){
		return stacktop ==-1;
	}
}

class MyQueen{
	MyStack stack1;
	MyStack stack2;
	int maxn ;
	
	public MyQueen(int n){
		stack1 = new MyStack(n);
		stack2 = new MyStack(n);
		maxn = n;
	}
	
	public void add(char c) throws Exception{
		stack1.push(c);
	}
	
	public char remove() throws Exception{
		if(stack2.isEmpty()){
			while(!stack1.isEmpty()){
				stack2.push(stack1.pop());
			}
		}
		return stack2.pop();
		
	}
	
	public char Max(){
		return stack1.Max()>stack2.Max()?stack1.Max():stack2.Max();
	}
}