AA Tree

Based on“Data Structures and Algorithm Analysis Edition 3.2 (C++ Version)” from C. A. Shaffer

Proporties

AA Tree is a variation of the red-black tree, whose red nodes can only be added as a right subchild, which greatly simplifies the maintenance operations.
AA trees require O(log(N)) bits of metadata per node, in the form of an integer “level”. The following invariants hold for AA trees:
- The level of every leaf node is one.
- The level of every left child is exactly one less than that of its parent.
- The level of every right child is equal to or one less than that of its parent.
- The level of every right grandchild is strictly less than that of its grandparent.
- Every node of level greater than one has two children.
According to the invariants above, if all the edges point to the red nodes are drawn horizontally, the leaf nodes will be at the same level.

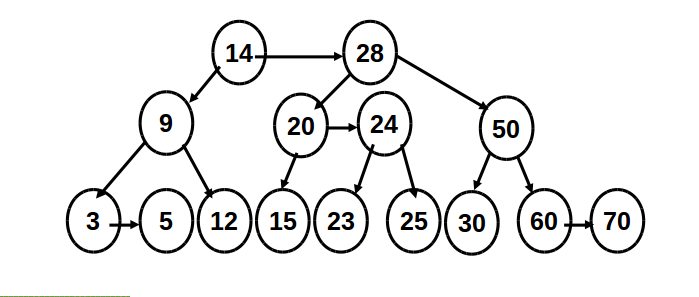
Individual right horizontal links are allowed, but consecutive ones are forbidden; all left horizontal links are forbidden. When forbidden case rises, rebalancing is needed.

Operation

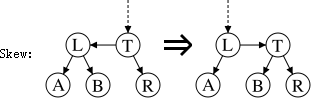
Skew

Skew operation is used for dealing with the first forbidden case. Skew is a right rotation to replace a subtree containing a left horizontal link with one containing a right horizontal link instead.

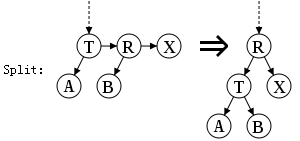
Split

Split operation is used for dealing with the second forbidden case. Split is a left rotation and level increase to replace a subtree containing two or more consecutive right horizontal links with one containing two fewer consecutive right horizontal links.

Insert

Insertion begins with the normal binary tree search and insertion procedure. Then check forbidden cases and take corresponding operations, until all the forbidden cases are solved.

Remove

The first step of removing is the same as that in a BST: if internal, exchange it with the leftest leaf in the right subtree, then delete the leaf.
After a removal, the first step to maintaining tree validity is to lower the level of any nodes whose children are two levels below them, or who are missing children. Then, the entire level must be skewed and split. This approach was favored, because when laid down conceptually, it has three easily understood separate steps:
1. Decrease the level, if appropriate.
2. Skew the level.
3. Split the level.
Here’s an example:
Try to delete node 15:

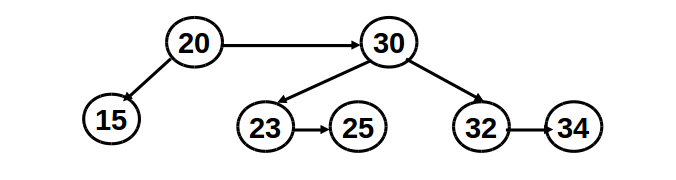
Do skew to node 30, solve the left horizontal link problem from 30 to 23:

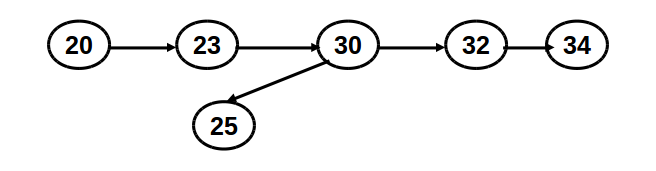
Do skew to node 30, solve the left horizontal link problem from 30 to 25:

Do split to node 25:

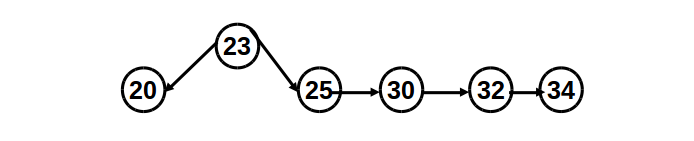
Finish.

Performance

The performance of an AA tree is equivalent to the performance of a red-black tree. While an AA tree makes more rotations than a red-black tree, the simpler algorithms tend to be faster, and all of this balances out to result in similar performance.