整数划分

1.问题描述

输入：

每组输入是两个整数n和k。(1 <= n <= 50, 1 <= k <= n) 

输出：

对于每组输入，请输出六行。 

第一行： 将n划分成若干正整数之和的划分数。 

第二行： 将n划分成k个正整数之和的划分数。 

第三行： 将n划分成最大数不超过k的划分数。 

第四行： 将n划分成若干奇正整数之和的划分数。 

第五行： 将n划分成若干不同整数之和的划分数。 

第六行： 打印一个空行。

算法思想：

a.将n划分成若干正整数之和的划分数:

将数字n进行分裂，其实这是一个穷举的过程，只是我们需要在分裂的过程中对被分裂的数字加上一些限制，这样就可以避免重复的分裂，例如5，我们要分解得到2+3，但是不能允许3+2的分裂出现，因为这样会重复，使算法的时间复杂度增大。简言之，就是要保证分裂出来的数据按递增排序，这样就可以有效地避免重复。算法实现是，规定一个start与end，对当前分裂数字只允许其分裂于范围start到end/2之间。举例说明

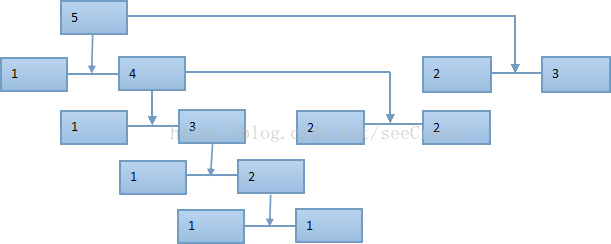
图一

图一的显示了数字5的划分过程，这是一个由两个参数start与end控制的递归过程(递归中有迭代，5和4的划分可以看出)，它有效地避免了重复，大大降低了时间复杂度。

代码：

int allpart_recur(int start, int end)
{
		int i = 0;
		int a = 0;
		if(start == end || (start !=1 && start + 1 == end))
		{
			return 0;
		}
		for(i = start; i <= end / 2; i++)
		{
			a++;
			a += allpart_recur(i, end - i);
		}
		return a;
}

复杂度分析：

由算法时间为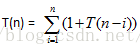,可以近似得出算法时间复杂度为O(n^2)。

a.将n划分成k个正整数之和的划分数:

这种情况采用动态规划的方法，定义一个递归式，然后迭代地求出结果，递归式如下：

dp[n][k] = dp[n - k][k] + dp[n - 1][k - 1]

dp[i][j] = 1      j = 1 或 i = j

解释：

dp[n - k][k]表示将数字n-k分配为k个数之和的划分数

dp[n - 1][k - 1]表示将n - 1 分配为k - 1个数的划分数

dp[n][k]表示将数字n划分为k个数的划分数

第一个数组表示将n划分为不包含1的划分数，相当于已经给k个碗中各放入了1个馒头，此时还剩n - k个馒头，再讲这n - k个馒头以某种方式放入到k个碗中，这就实现了将n划分为不包含1的划分数

第二个数组表示将n划分为至少包含一个1的划分数，相当于已经将一个馒头放入了某个碗中，然后将剩下的n - 1个馒头以某种方式放入到剩下的k - 1个碗中。这就实现了将n划分为至少包含一个1的划分数

这种表达式的正确性：

“不包含1”与“至少包含一个1”刚好是互补的两个条件，他们组合在一起就是所有可能的情况，至于为什么要选择这两个互补条件，是为了递归地减小n与k的值，使他们达到我们的终止条件，即第二个表达式。

代码：

int partknum(int n, int k)
{
		int dp[n+1][k+1];
		int i = 0;
		int j = 0;
		for(i = 0; i <= n; i++)
		{
			for(j = 0; j <= k; j++)
			{
				dp[i][j] = 0;
			}
		}
		for(i = 1; i <= n; i++)
		{
			dp[i][1] = 1;
		}
		for(i = 1; i <= k; i++)
		{
			dp[i][i] = 1;
		}
		dp[0][0] = 0;
		for(i = 2; i <= n; i++)
		{
			for(j = 2;(j <= i) && (j <= k); j++)
			{
				dp[i][j] = dp[i - j][j] + dp[i - 1][j - 1];
			}
		}
		return dp[n][k];
}

算法时间复杂度：

有算法描述可知问题规模为n*k，并且每一个值的求解时间为O(1),所以时间复杂度为O(nk)。

a.将n划分成最大数不超过k的划分数:

这种情况采用了与a类似的做法，区别在与在a的基础上多增加了一个限制条件，保证所划分的数不超过k

代码：

int allpart_recur_maxk(int start, int end, int k)
{
		int i = 0;
		int a = 0;
		if(start == end || (start !=1 && start + 1 == end))
		{
			return 0;
		}
		for(i = start; i <= k && i <= end / 2; i++)
		{
			if(end - i <= k)
			{
				a++;
			}
			a += allpart_recur_maxk(i, end - i, k);
		}
		return a;
}

在上面的代码中只要保证i <= k，end - i <= k就可以保证分配出的所有数字不超过k。

算法时间复杂度：

与a的情况相同时间复杂度为O(n^2)。

a.将n划分成若干奇正整数之和的划分数:

在这种情况下，采用了与情况b类似的做法，定义一个递归式，用迭代的方式实现算法，递归式如下：

g[i][j] = f[i - j][j]

f[i][j] = f[i - 1][j - 1] + g[i - j][j]

其中g[i][j]表示将i划分为j个偶数的划分数

其中f[i][j]表示将i划分为j个奇数的划分数

第一个表达式的意思就是 将i划分为j个偶数的划分数与将i-j划分为j个奇数的划分数是相同的，当然，因为每一个奇数加上1过后就是偶数。相当于我们已经给j个碗中各放入了一个馒头，此时，再将剩下的i-j个馒头放入j个碗中，要求每一个碗中放入奇数个馒头，这样就实现了将i个馒头放入j个碗中，每个碗中有偶数个馒头。

第二个表达式的意思是，将i划分为j个奇数的划分数等于将i-1划分为j-1个奇数的划分数与将i-j划分为j个偶数的划分数之和。很显然此处又是一个互补条件情况之和等于整体情况的用法。f[i-1][j-1]表示将i划分为j个奇数，并且至少有一个是1。

g[i - j][j]表示将i划分为j个奇数，并且不包含1，分析方法与a类似。

代码：

int partoddnumk(int n, int k)
{
		int i = 0;
		int j = 0;
		int odd[n + 1][k + 1]; 
		int even[n + 1][k + 1];
		for(i = 0; i <= n; i++)
		{
			for(j = 0; j <= k; j++)
			{
				odd[i][j] = 0;
				even[i][j] = 0;
			}
		}
		for(i = 0; i <= n; i++)
		{
			for(j = 0; j <= k; j++)
			{
				if(i == j)
				{
					odd[i][j] = 1;
				}
			}
		}
		for(i = 1; i <= n; i += 2)
		{
			odd[i][1] = 1;
		}
		for(i = 2; i <= n; i += 2)
		{
			even[i][1] = 1;
		}
		for(i = 2; i <= n; i++)
		{
			for(j = 2; j < i && j <= k; j++)
			{
				even[i][j] = odd[i - j][j];
				odd[i][j] = odd[i -1][j - 1] + even[i - j][j];
			}
		}	
		return odd[n][k];
}
int partoddnum(int n)
{	
		int all = 0;
		int i = 1;
		for(i = 1; i <= n; i++)
		{
			all += partoddnumk(n,i);
		}
		return all;
}

算法时间复杂度：

a.将n划分成若干不同整数之和的划分数:

对于这种情况，使用了与a相同的策略，也是在a的基础上增加了限制，即保证数据不重复出现。

代码：

int allpart_recur_dif(int start, int end)
{
		int i = 0;
		int a = 0;
		if(start == end || (start !=1 && start + 1 == end))
		{
			return 0;
		}
		if(end % 2)
		{
			for(i = start; i <= end / 2; i++)
			{
				a++;
				a += allpart_recur_dif(i + 1, end - i);
			}
		}
		else
		{
			for(i = start; i < end / 2; i++)
			{
				a++;
				a += allpart_recur_dif(i + 1, end - i);
			}
		}
		return a;
}
int partdifnum(int n)
{
		return 1 + allpart_recur_dif(1, n);
}

如代码所示此处主要在向下递归时将向下传递的数由i变成i+1，原来的目的只是非递减，而现在是严格递增(无重复)。

算法时间复杂度：

这种情况下与a的情况一致，算法时间为O(n^2)。