算法导论第一部分学习笔记

算法是处理数据的计算过程，在计算中明智的使用时间、空间等资源

数据结构是储存数据的方式，主要目的是为了满足占用空间、查找速度、插入速度中的一部分

循环不变式

从一道有趣的题目开始

布口袋中有黑，白两色小球，现将手放入袋中每次摸出两个，如果两球同
色就都不放回袋中，如果两球异色就将白球放回，由于每次至少减少一
个，所以袋中的球必然越来越少。现问:如果袋中最后剩下一个球，此球
的颜色与开始时袋中黑、白球的个数有什么关系？按照一般的思路，此题
非常复杂，难以解决。多次重复摸球及放回的动作构成了一个循环过程。
如果我们有意识地寻找循环过程中不变的性质，就会发现,在循环过程中,
白球个数的奇偶性保持不变,因为,每次取出的白球的个数或是零或是2.因
此,如果开始时白球的个数为奇数,那么剩下的一球为白球。如果开始时白
球的个数为偶数，那么剩下的一球为黑球

循环不变式的作用是让我们理解并且证明算法的正确性（因为程序只要不是O(1)的，都可以看做循环的变种）

循环不变式总的来说是一个判断语句，她的主要性质如下：

1，初始化：在循环开始之前，循环不变式判断为true
2，保持：在一次迭代的前后，她都判断为true
3，终止：在循环终止时，不变式为我们提供一个有用的性质

举几个例子：
1，在算法导论中，插入排序的循环不变式为数组A[1,…,j]都是已经排好序的数组，在开始到结束都满足这个性质
2，题目2.1-3，循环不变式为A[1,…,j]中都不包含val
3，在上面那道有趣的题目中，循环不变式为白球个数的奇偶性保持不变

求解递归式

当一个函数包含对其自身的调用时，我们就可以使用一个递归式来表示，例如：

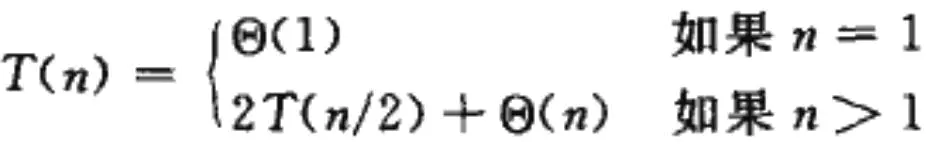
那么如何算出形如该函数的时间复杂度呢，算法导论给出了三个方法：主方法、递归树法、代入法

代入法

根据过往的经验来猜测递归式的解O(x)，同时，如果可以寻找一个数c，证明T(x) <= cO(x)，则可以确定界

例如：T(n) = 2T(n/2)+n，我们猜测解是O(nlgn)
代入可知T(n) <= 2c(n/2)lg(n/2)+n <= cnlgn-cnlg2+n = cnlgn-cn+n
因此T(n) <= O(nlgn)，所以我们的猜测成立

递归树法

将递归式转化为树形结构，树中的结点代表在不同递归层次付出的代价，最后利用对和式限界的技术来解出递归式

在第二章分析分治算法的时候就用到了递归树法，比如求解下面递归式

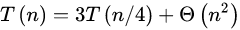
画出图像：

每一层每个节点的数字代表了执行此函数使用的代价，而右边代表了这一层的总代价，将右边每一层代价加起来就找到了这个递归树的总代价

注意，最后一层的时间复杂度是常数，所以只要计算出有多少的节点就行，因为树的深度为log4n，每层数目是上层的三倍，所以得出nlog43

我们通过找规律就能直接得出这个公式，甚至可以把公式背下来（就是下面介绍的主方法），很多情况下通过递归树是解决不了问题的。做过后面练习题就知道，最后的解会出现形如3^(lgn+1)这种鬼东西，完全没有意义

因此在求解之前，需要先进行缩放，我们可以以此来确定解的上界或者下界

对T(n) = T(n/3) + T(2*n/3) + O(n)，时间复杂度是nlgn
对T(n) = T(n/2) + O(n ^ 2)，时间复杂度为 n ^ 2

主方法

主方法是一个公式，形如T(n) = a * T(n/b) + f(n)的递归式都可以使用主方法求解

主方法原理式使用递归树解出适用于任意a、b和f(n)的统一解，计算所有中间结点和叶子结点的代价和，推导出简单的结果

图中说总代价等于一个奇怪的玩意，但是先辈们已经将这个结论简化了，他们发现上层代价与底层总代价的大小关系决定了递归式的解，因此只要直接记住结论即可，我们记中间累加式为g(n)：

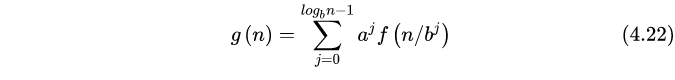
1，如果底层代价较大的话，g(n)以及递归式的解就为底层代价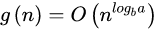

2，如果两个一样大，g(n)为底层代价乘lgn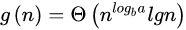
3，如果f(n)比较大，即上层的代价大的话，需要满足对于某个常数c<1和所有足够大的n满足如下公式

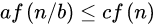
此时，可以得出

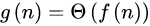
渐进符号

我们在算法书上最常见的是Θ符号（读作/ˈθiːtə/，theta），它定义了上界和下界，f(n)位于上界和下界之间，且包含等号，使用官方语言说是：

若存在正常数c1、c2,使得对于足够大的n, f (n)能“夹入”c1g(n)和c2g(n)之间，则f (n)属于集合Θ（g(n)）

其他四个分别是：
O，大Oh，定义了函数的上界，不定义函数的下界；
o，小Oh，定义了函数的上界，不过它不包含等于，是一种不精确的上界，比如：2n = o(n^2)，2n != o(n)；
Ω，大Omega，定义了函数的下界，不定义函数的上界；
ω，小Omega，同样定义的是下界，只不过不包含等于，是一种不精确的下界

但是，平时我们使用的最多的却是O。因为在有些场景Θ是不正确的，描述算法时，算法的最好复杂度可能低于这个界，例如插入排序的时间复杂度是O(N ^ 2)而不是Θ(N ^ 2)，因为其最好时为Θ(N)

优雅的写法

收录在第一部分遇到的题目的简洁而易读的写法

多重判断拆分

某些问题需要进行嵌套判断，寻找到一些可以移除的性质一层一层进行处理

eg：
考虑把两个n位二进制整数加起来的问题，这两个整数分别存储在两个n元数组A和B中。这两个整数的和应按二进制形式存储在一个（n+1）元数组C中

ADD-BINARY(A, B):
  C = new integer[A.length + 1]

  carry = 0
  for i = 1 to A.length
      C[i] = (A[i] + B[i] + carry) % 2  // remainder
      carry = (A[i] + B[i] + carry) / 2 // quotient
  C[i] = carry

  return C

哨兵牌

为了避免在一些判断，我们在适当的时候加入哨兵牌，它包含一个特殊的值，用于简化代码

eg：
合并两个已排序的子序列以产生已排序的新序列

这里我们使用∞作为哨兵值，结果每当显露一张值为∞的牌，它不可能为较小的牌，除非两个序列都已经显露出其哨兵牌