BZOJ 3227 [Sdoi2008] 红黑树(tree)

Description

　　红黑树是一类特殊的二叉搜索树，其中每个结点被染成红色或黑色。若将二叉搜索树结点中的空指针看作是指向一个空结点，则称这类空结点为二叉搜索树的前端结点。并规定所有前端结点的高度为-1。

　　一棵红黑树是满足下面“红黑性质”的染色二叉搜索树：

　　(1) 每个结点被染成红色或黑色；

　　(2) 每个前端结点为黑色结点；

　　(3) 任一红结点的子结点均为黑结点；

　　(4) 在从任一结点到其子孙前端结点的所有路径上具有相同的黑结点数。

　　从红黑树中任一结点x出发(不包括结点x)，到达一个前端结点的任意一条路径上的黑结点个数称为结点x的黑高度，记作bh(x)。红黑树的黑高度定义为其根结点的黑高度。

　　给定正整数N，试设计一个算法，计算出在所有含有N个结点的红黑树中，红色内结点个数的最小值和最大值。

 

Input

　　输入共一个数N。

 

Output

 

　　输出共两行。

　　第一行为红色内结点个数的最小值，第二行为最大值。

 

Sample Input

8

Sample Output

1
4

HINT

对于 100% 的数据，1≤N≤5000

Source

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

神奇的贪心~

从叶子节点开始往上合并，那么一棵有n个节点的树的叶子结点数量m=n+1。

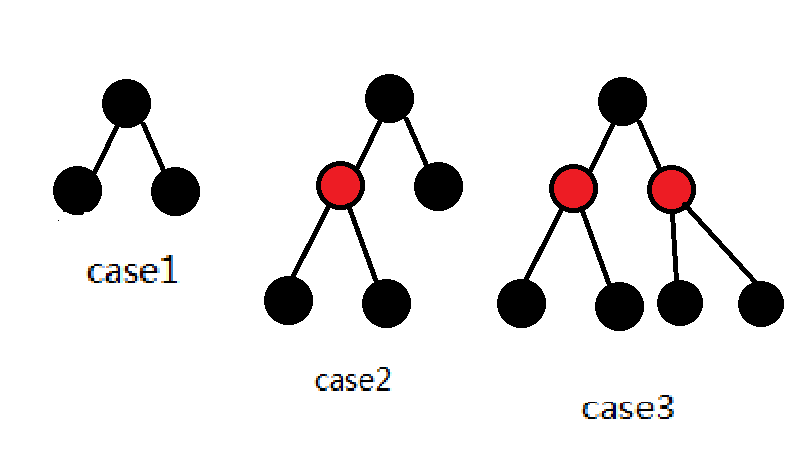
假设刚开始所有m个点都是黑点，那么我们要做的就是压这些点，把其中一些压成红色的，共有3种情况：

（1）两个黑点压成一个黑点；

（2）三个黑点压成一黑一红；

（3）四个黑点压成一黑两红.

所以用位运算贪心一下就好了~

位运算要加括号！位运算要加括号！位运算要加括号！

#include<cstdio>

int n,m,ans;

int main()
{
	scanf("%d",&n);
	m=n+1;
	while(m>1)
	{
		ans+=m&1;m>>=1;
	}
	printf("%d\n",ans);
	m=n+1;ans=0;
	while(m>1)
	{
		if(m==2) ans++;
		if((m&3)==1) ans+=m/4*2-1,m/=4,m++;
		else if((m&3)==2) ans+=m/4*2,m/=4,m++;
		else if((m&3)==3) ans+=m/4*2+1,m/=4,m++;
		else ans+=m/4*2,m/=4;
	}
	printf("%d\n",ans);
	return 0;
}