POJ 2411 Mondriaan's Dream 解题报告

最新推荐文章于 2018-10-25 13:17:00 发布

原创最新推荐文章于 2018-10-25 13:17:00 发布 · 1.1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#状态压缩 #DP

ACM 专栏收录该内容

224 篇文章

订阅专栏

本文介绍了一道有趣的编程题目 Mondriaan's Dream 的解题思路及优化过程，涉及状态压缩和动态规划技术。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Mondriaan's Dream

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 10132		Accepted: 5865

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

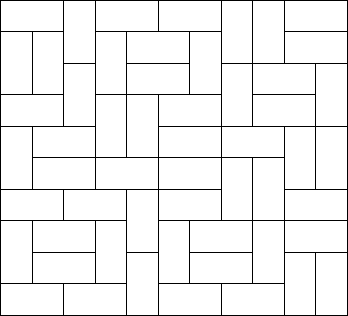For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

Sample Output

Source

Ulm Local 2000

解题报告：很有意思的一道题。

在状态压缩专题里刷的，所以首先想到的就是类似于炮兵阵地的状态压缩和转移。

在一行中，我们用当前行1下一行0表示竖着放的砖，用00表示横着放的砖头。而两行的状态a，b，如果a|b==0，说明竖着的砖头不冲突。并且如果a|b的二进制形式中所有的0都是连续偶数的，如1001，就表示剩下的我们可以横着放，a，b可转移。

然后就是代码：

#include <cstring>
#include <cstdio>
#include <algorithm>
#include <iostream>
using namespace std;

const int maxn=1<<11;
#define LL long long 
LL dp[12][maxn];
LL res[12][12];
int n,m;

bool ok(int a,int b)
{
	if(a&b) return false;
	a|=b;

	bool two=false;
	int t=m;
	while(t--)
	{
		if(!(a&1))
		{
			if(two)
				two=false;
			else
				two=true;
		}
		else if(two)
			return false;
		a>>=1;
	}
	if(two) return false;
	return true;
}

int main()
{
	memset(res,-1,sizeof(res));
	while(scanf("%d%d",&n,&m),n||m)
	{
		if(n*m%2)
		{
			puts("0");
			continue;
		}
		else if(~res[n][m])
		{
			printf("%I64d\n",res[n][m]);
			continue;
		}
		memset(dp,0,sizeof(dp));
		dp[0][0]=1;

		int total=1<<m;
		for(int i=1;i<n;i++)
			for(int j=0;j<total;j++)
				for(int k=0;k<total;k++) if(ok(k,j))
					dp[i][j]+=dp[i-1][k];
		LL ans=0;
		for(int i=0;i<total;i++) if(ok(i,0))
			ans+=dp[n-1][i];
		printf("%I64d\n",res[n][m]=ans);
	}
}

这是最初的代码，600MS+。因为基本没有优化的。

后来看到一个优化，在遍历状态j时，可以判断dp[i][j]是否等于0，等于0就不用计算了。大概优化到300MS。

再想一下，整个图形的对称性很强。例如，当前行1100与0011状态的方法数量一定是一致的。

上下也可以对称的，能不能根据这个来优化呢？例如7*10，我们遍历到第4行，下面还有3行。而3行的状态都求过了，直接判断是否可行并相乘即可。

实现时略有区别。7*10的例子只算到第3行，直接判断两个第3行的状态能否构成一个新行即可。代码如下：

#include <cstring>
#include <cstdio>
#include <algorithm>
#include <iostream>
using namespace std;

#define LL long long 
LL dp[12][1<<11];
int n,m;

bool ok(int a,int b)
{
	if(a&b) return false;
	a|=b;

	bool two=false;
	int t=m;
	while(t--)
	{
		if(!(a&1))
		{
			if(two)
				two=false;
			else
				two=true;
		}
		else if(two)
			return false;
		a>>=1;
	}
	if(two) return false;
	return true;
}

int main()
{
	while(scanf("%d%d",&n,&m),n||m)
	{
		if( n%2 && m%2 ) { puts("0"); continue; }

		memset(dp,0,sizeof(dp));
		dp[0][0]=1;

		int total=1<<m;
		int a=n/2,b=(n-1)/2;
		for(int i=1;i<=a;i++)
			for(int j=0;j<total;j++) if(dp[i-1][j])
				for(int k=0;k<total;k++) if(ok(k,j))
					dp[i][k]+=dp[i-1][j];

		LL ans=0;
		for(int j=0;j<total;j++) if(dp[a][j])
			for(int k=0;k<total;k++) if(ok(k,j))
				ans+=dp[a][j]*dp[b][k];
		printf("%I64d\n",ans);
	}
}

上面的代码已经在100MS以下了。

网上也有插头DP的方法。因为还没开始学习插头DP，就研究了一下。代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

long long dp[2][1<<11];

int main()
{
	int n,m;
	while(scanf("%d%d",&n,&m),(n||m))
	{
		int total=1<<m;
		int pre=0,now=1;
		memset(dp[now],0,sizeof(dp[now]));
		dp[now][0]=1;

		for(int i=0;i<n;i++)
			for(int j=0;j<m;j++)
		{
			swap(now,pre);
			memset(dp[now],0,sizeof(dp[now]));

			for(int S=0;S<total;S++) if( dp[pre][S] )
			{
				dp[now][S^(1<<j)]+=dp[pre][S];
				if( j && S&(1<<(j-1)) && !(S&(1<<j)) )
					dp[now][S^(1<<(j-1))]+=dp[pre][S];
			}
		}

		printf("%lld\n",dp[now][0]);
	}
}

时效更夸张，16MS。总之这道题很有意思，Discuss里也很好玩。