数据结构与算法基础 第六章 图 思维导图
最新推荐文章于 2019-12-24 08:28:29 发布
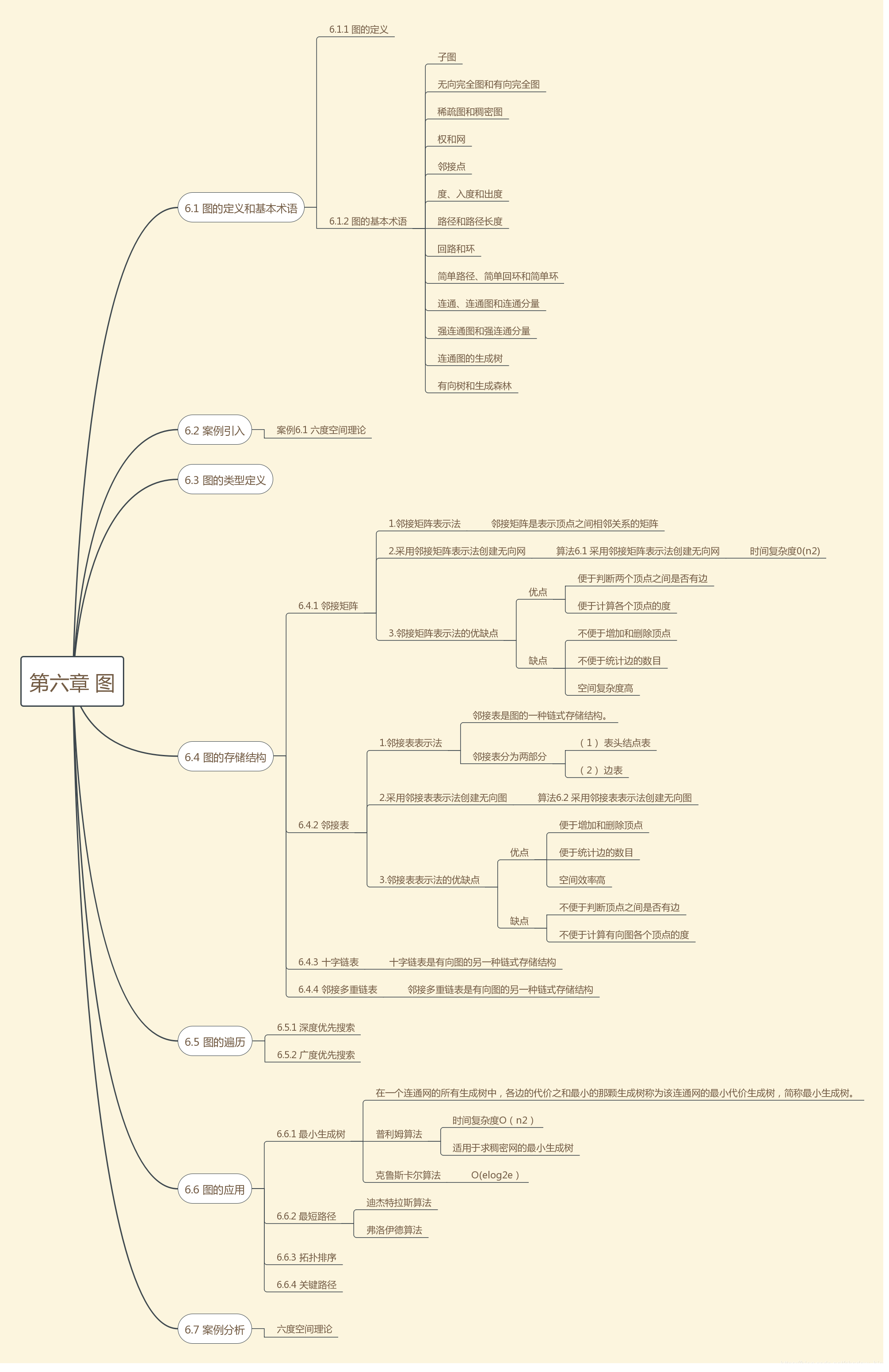
 该博客围绕数据结构中的图展开,以思维导图形式呈现相关内容,涵盖图在数据结构领域的知识要点,有助于理解图的概念、特性及应用等信息技术相关内容。
该博客围绕数据结构中的图展开,以思维导图形式呈现相关内容,涵盖图在数据结构领域的知识要点,有助于理解图的概念、特性及应用等信息技术相关内容。
 该博客围绕数据结构中的图展开,以思维导图形式呈现相关内容,涵盖图在数据结构领域的知识要点,有助于理解图的概念、特性及应用等信息技术相关内容。
该博客围绕数据结构中的图展开,以思维导图形式呈现相关内容,涵盖图在数据结构领域的知识要点,有助于理解图的概念、特性及应用等信息技术相关内容。

 6097
6097
 1305
1305
 455
455
 1314
1314
 440
440
 433
433
 1012
1012
 795
795

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


