2014蓝桥杯决赛试题及答案

猜灯谜

A村的元宵节灯会上有一迷题：

请猜谜 * 请猜谜 = 请边赏灯边猜

小明想，一定是每个汉字代表一个数字，不同的汉字代表不同的数字。

请你用计算机按小明的思路算一下，然后提交“请猜谜”三个字所代表的整数即可。

请严格按照格式，通过浏览器提交答案。

注意：只提交一个3位的整数，不要写其它附加内容，比如：说明性的文字。

答案：897

直接for加判断就好

加密

在对文本进行简单加密的时候，可以选择用一个n位的二进制数，对原文进行异或运算。
解密的方法就是再执行一次同样的操作。

加密过程中n位二进制数会循环使用。并且其长度也可能不是8的整数倍。

下面的代码演示了如何实现该功能。

请仔细阅读，填写空缺的代码（下划线部分）。

注意：请把填空的答案（仅填空处的答案，不包括题面）存入考生文件夹下对应题号的“解答.txt”中即可。
直接写在题面中不能得分。

void f(char* buf, unsigned char* uckey, int n)
{
    int i;
    for(i=0; i<n; i++)
        buf[i] = buf[i] ^ uckey[i];
}

int main(int argc, char* argv[])
{
    char p[] = "abcd中国人123";  // 待加密串

    char* key = "11001100010001110";  //以串的形式表达的密匙，运算时要转换为按位存储的形式。

    int np = strlen(p);
    int nk = strlen(key);
    unsigned char* uckey = (unsigned char*)malloc(np);  

    // 密匙串需要按位的形式循环拼入 uckey中
    int i;
    for(i=0; i<np*8; i++)
    {
        if(key[i%nk]=='1')
            ____________________________________________;  // 填空1
        else
            ____________________________________________;  // 填空2

    }

    f(p, uckey, strlen(p));
    f(p, uckey, strlen(p));

    printf("%s\n", p);

    free(uckey);

    return 0;
}

答案：

 // 密匙串需要按位的形式循环拼入 uckey中  
    int i;  
    for(i=0; i<np*8; i++)  
    {  
        if(key[i%nk]=='1')  
        {  
            uckey[i / 8] = (uckey[i / 8] << 1) | 0x01;  // 填空1  
            //uckey[i/8] |= (unsigned char)0x80 >> (i%8); //标准答案  
        }  
        else  
        {  
            uckey[i / 8] = uckey[i / 8] << 1;  // 填空2  
            //uckey[i/8] &= ~((unsigned char)0x80 >> (i%8)); //标准答案  
        }  

    }  

公倍数

为什么1小时有60分钟，而不是100分钟呢？这是历史上的习惯导致。
但也并非纯粹的偶然：60是个优秀的数字，它的因子比较多。
事实上，它是1至6的每个数字的倍数。即1,2,3,4,5,6都是可以除尽60。

我们希望寻找到能除尽1至n的的每个数字的最小整数。

不要小看这个数字，它可能十分大，比如n=100, 则该数为：
69720375229712477164533808935312303556800

请编写程序，实现对用户输入的 n （n<100）求出1~n的最小公倍数。

例如：
用户输入：
6
程序输出：
60

用户输入：
10
程序输出：
2520

要求考生把所有函数写在一个文件中。调试好后，存入与考生文件夹下对应题号的“解答.txt”中即可。
相关的工程文件不要拷入。
对于编程题目，要求选手给出的解答完全符合ANSI C标准，不能使用c++特性；
不能使用诸如绘图、中断调用等硬件相关或操作系统相关的API。

答案：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;

const int N = 105;
int n;
int a[N][50];
int b[N] = {0};

void multiply()
{
    int i,j,k;
    memset(a,0,sizeof(a));
    for(i=3; i<=100; i++)
    {
        /*
        下面的是直接按平常的乘法，乘数的一位乘以被乘数的每一位并处理进位；另外是乘数整体乘以被乘数的每一位最后统一处理进位
        */
        int temp = 0; 
        a[i][0] = 1;//很重要 
        for(j=2; j<=i; j++)
        {
            int  c = 0; 
            for(k=0; k<50; k++)//最大不超过160位 ，安的是100!,最后除以3等50 
            {
                temp = a[i][k]*b[j] + c;
                a[i][k] = temp%1000;
                c = temp/1000;
            }          
        }
    }
}

void printData(int n)
{
    int i,j,k;
    for(i=49; i>=0; i--)
    if(a[n][i])
        break;
    cout<<a[n][i];//第一个不输出前导0 
    for(j=i-1; j>=0; j--)
        printf("%03d",a[n][j]);
    cout<<endl;   
}

int main()
{
    int i, j, k;
    for(i=0; i<N; i++)
            b[i] = i;
    for(i=2; i<N; i++)
        for(j=i+1; j<=N; j++)
        {
            if(b[j]%b[i]==0)
                b[j] /= b[i];
            //cout<<b[j]<<endl;
        }
    //for(i=0; i<100; i++)
      //  cout<<b[i]<<endl;
    //while(1);
    multiply();

    while(cin>>n)
    {

        if(n==1||n==2)
        {
            cout<<n<<endl;
            continue;
        }

        printData(n);
    }
    return 0;
}

高僧斗法

古时丧葬活动中经常请高僧做法事。仪式结束后，有时会有“高僧斗法”的趣味节目，以舒缓压抑的气氛。
节目大略步骤为：先用粮食（一般是稻米）在地上“画”出若干级台阶（表示N级浮屠）。又有若干小和尚随机地“站”在某个台阶上。最高一级台阶必须站人，其它任意。
两位参加游戏的法师分别指挥某个小和尚向上走任意多级的台阶，但会被站在高级台阶上的小和尚阻挡，不能越过。两个小和尚也不能站在同一台阶，也不能向低级台阶移动。
两法师轮流发出指令，最后所有小和尚必然会都挤在高段台阶，再也不能向上移动。轮到哪个法师指挥时无法继续移动，则游戏结束，该法师认输。
对于已知的台阶数和小和尚的分布位置，请你计算先发指令的法师该如何决策才能保证胜出。
输入数据为一行用空格分开的N个整数，表示小和尚的位置。台阶序号从1算起，所以最后一个小和尚的位置即是台阶的总数。（N<100, 台阶总数<1000）
输出为一行用空格分开的两个整数: A B, 表示把A位置的小和尚移动到B位置。若有多个解，输出A值较小的解，若无解则输出-1。
例如：
用户输入：
1 5 9
则程序输出：
1 4

再如：
用户输入：
1 5 8 10
则程序输出：
1 3

资源约定：
峰值内存消耗 <64M

CPU消耗 < 1000ms

答案：（好像用到了尼姆定理）

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#include<limits.h>
using namespace std;

int t[1111];
int b[1111];
int c[1111];

void xiazi(int sum)
{
    for(int i= 1; i< sum; i++)
        for(int j= 1; j<= b[i]; j++)
        {
            int xixi;
            if(i%2)
                xixi= c[i]^(b[i]-j);    
            else
                xixi= c[i-1]^(b[i-1]+j);
            if(xixi==0)
            {
                printf("%d %d\n",t[i],t[i]+j);  
                return; 
            }
        }
    printf("-1\n");
    return; 
}


int main()
{
    int a;
    char ch;
    scanf("%d%c",&a,&ch);
    int sum= 1;
    t[sum]= a;
    c[0]= 0;
    while(ch!='\n')
    {
        scanf("%d%c",&a,&ch);
        sum++;
        t[sum]= a;
    }
    sort(t+1, t+ sum + 1);
    for(int i= 2; i<= sum; i++)
    {
        b[i-1]= t[i]- t[i-1] - 1;
        if((i-1)%2)
            c[0]= c[0]^b[i-1]; 
    }
    for(i= 1; i< sum; i+=2)
        c[i]= c[0]^b[i];
    if(c[0]==0)
        printf("-1\n");
    else
        xiazi(sum); 
    return 0;
}

方格填数

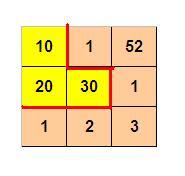
如下图所示，3 x 3 的格子中填写了一些整数。
+–*–+–+
|10* 1|52|
+–**–+
|20|30* 1|
*–+
| 1| 2| 3|
+–+–+–+
我们沿着图中的星号线剪开，得到两个部分，每个部分的数字和都是60。
本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。
如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割，则输出 0。

输入格式
程序先读入两个整数 m n 用空格分割 (m,n<10)。
表示表格的宽度和高度。
接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000。
输出格式
输出一个整数，表示在所有解中，包含左上角的分割区可能包含的最小的格子数目。

样例输入1
3 3
10 1 52
20 30 1
1 2 3
样例输出1
3

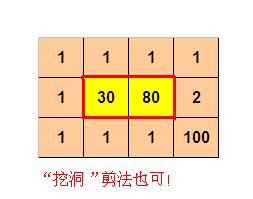
样例输入2
4 3
1 1 1 1
1 30 80 2
1 1 1 100
样例输出2
10

答案：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#define N 10

int map[N][N]={0};
int vis[N][N];
int count=0;//记录解得节点数
int mincount=1000;//记录最小的节点数
int result=0;//记录搜索过程中的结果和
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
int half;

void mysearch(int i,int j,int n,int m);//回溯法进行搜索

int main()
{
    int m,n; //n：行，m：列
    int i,j,sum=0;
    int max=-1;
    scanf("%d%d",&m,&n);
    for(i=0;i<n;i++)
    {
        for (j=0;j<m;j++)
        {
            scanf("%d",&map[i][j]);
            if (max<map[i][j])
            {
                max=map[i][j];
            }
            sum+=map[i][j];
        }
    }
    half=sum/2;
    if(max>half) //最大值大于全体数字的一般，无解
    {
        printf("0\n");
        return 0;
    }

    memset(vis,0,sizeof(vis));
    i=j=0;
    mysearch(i,j,n,m);
    system("pause");
    return 0;
}

void mysearch(int i,int j,int n,int m) //回溯法进行搜索
{
    int x,y,newx,newy;   
    int r;
    x=i;
    y=j;

    if (i<0 || i>=n || j<0 || j>=m)
    {
        return;
    }

    if(vis[x][y]==0 && result+map[x][y] <= half)
    {
        printf("(%d,%d)\n",x,y);
        result+=map[x][y];
        vis[x][y]=1;
        count++;
    }
    else
    {
        return;
    }
    if (result==half)
    {

        if (count>n*m/2)
        {
            printf("%d\n",n*m-count);
        }
        else
        {
            printf("%d\n",count);
        }
        exit(0);
    }

    for (r=0;r<4;r++)
    {
        newx=x+dx[r];
        newy=y+dy[r];

        mysearch(newx,newy,n,m);
    }

    vis[x][y]=0;
    result=result-map[x][y];
    count--;
    return;
}