数据结构与算法学习笔记04（约瑟夫问题）

数据结构与算法学习笔记04（约瑟夫问题）

 

约瑟夫问题

据说著名犹太历史学家 Josephus有过以下的故事：

在罗马人占领乔塔帕特后，39个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus和他的朋友并不想遵从，Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

 

问题：

用循环链表模拟约瑟夫问题，把41个人自杀的顺序编号输出。

实现：

1、逻辑数组判断法，用C++实现。

#include <iostream>
using namespace std;
void main()
{
	int N = 0, C = 0;
	cout << "Please enter the number of people:N=";
	cin >> N;
	cout << "Please enter:C=";
	cin >> C;
	//i,j是角标 s是计数
	int i = 0, j = 0, n = N, s = 0;
	int *a = new int[N];
	for (i = 0; i < N; i++)
	{
		a[i] = 1;
	}

	//人全部是杀死，停止循环
	while (n!=0)
	{
		//s计数
		s += a[j];
		if (C == s)
		{
			//做标记 标记为杀死
			a[j] = 0;
			//置零
			s = 0;
			//杀死一个人 然后减1
			n--;
			if (n!=0)
			{
				//角标加1 打印当前位置
				cout << j + 1 << "->";
			}
			else
			{
				//打印结束
				cout << j + 1 << endl;
			}
		}
		//解决多圈循环后，角标的问题
		j = (j + 1) % N;
	}
	delete[]a;

2、 用循环链表实现

 

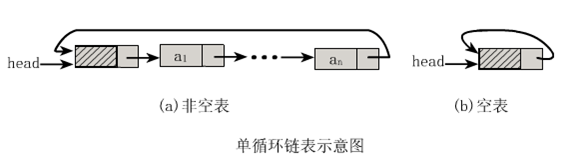
循环链表

将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表成为单循环链表，简称循环链表。

 

注意：

这里并不是说循环链表一定要有头结点。

其实循环链表的单链表的主要差异就在于循环的判断空链表的条件上，原来判断head->next是否为null，现在则是head->next是否等于head。

#include <iostream>
using namespace std;

/*宏定义和单链表类型定义*/
#define ListSize 100
typedef int DataType;
typedef struct Node
{
	DataType data;
	struct Node *next;
}ListNode, *LinkList;

//函数声明
LinkList CreateCycList(int n);//创建一个长度为n的循环单链表的函数声明
void Josephus(LinkList head, int n, int m, int k); //在长度为n的循环单链表中，报数为编号为m的出列
void DisplayCycList(LinkList head);//输出循环单链表

void main()
{
	LinkList h;
	int n, k, m;
	cout << "输入环中人的个数n=";
	cin >> n;
	cout << "输入开始报数的序号k=";
	cin >> k;
	cout << "报数为m的人出列m=";
	cin >> m;
	h = CreateCycList(n);
	Josephus(h, n, m, k);
}
void Josephus(LinkList head, int n, int m, int k)
/*在长度为n的循环单链表中，从第k个人开始报数，数到m的人出列*/
{
	ListNode *p, *q;
	int i;
	p = head;
	q = head;
	for (i = 1; i < k; i++)     /*从第k个人开始报数*/
	{
		q = p;
		p = p->next;
	}
	while (p->next != p)
	{
		for (i = 1; i < m; i++) /*数到m的人出列*/
		{
			q = p;
			p = p->next;
		}
		q->next = p->next;  /*将p指向的结点删除，即报数为m的人出列*/
		cout << p->data<<" ";
		free(p);
		p = q->next;           /*p指向下一个结点，重新开始报数*/
	}
	cout << p->data << endl;//输出最后一个结果
}

//创建一个循环链表
LinkList CreateCycList(int n)
/*宏定义和单链表类型定义*/
{
	LinkList head = NULL;
	ListNode *s, *r;
	r = NULL;
	int i;
	for (i = 1; i <= n; i++)
	{
		//创建后一个新的节点
		s = (ListNode*)malloc(sizeof(ListNode));
		s->data = i;
		s->next = NULL;
		if (head == NULL)
		{
			head = s;
		}
		else
		{
			r->next = s;
		}
		r = s;
	}
	//循环链表
	r->next = head;
	return head;
}