基本汉诺塔问题及其扩展问题（4个杆）

一 基本问题

有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

1. 每次只能移动一个圆盘；
2. 大盘不能叠在小盘上面。

提示：可将圆盘临时置于B杆，也可将从A杆移出的圆盘重新移回A杆，但都必须遵循上述两条规则。

问：如何移？最少要移动多少次？

三个圆盘：

定义hannoi(n,a,b,c)为将n个圆盘从a杆移动到c杆，借助b杆（不然无法完成移动）。(当n=1的时候，可以直接移动)

定义move(i,a,c)为将第i个圆盘从a杆直接移动到c杆（在满足上述规则2的情况下）。

现在只考虑如何将最大的圆盘n从a杆移动到c杆，显然在只有在c杆为空的情况下，移动才合法，也就是必须先将第1至n-1号圆盘先从a杆移动到b杆，借助c杆。然后才可以将最大的n号圆盘移动到c杆。

从而，显然得出了递归关系：

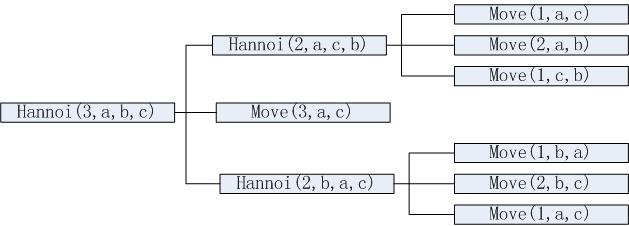
hannoi(n,a,b,c)=hannoi(n-1,a,c,b)+move(n,a,c)+hannoi（n-1,b,a,c）

对应的文字叙述为：

要将n个圆盘从a杆移动到c杆，借助b杆。（1）可以先将第1至n-1号圆盘，从a杆移动到b杆，借助c杆。然后（2）将第n号圆盘从a杆直接移动到c杆。最后（3）将第1至n-1号圆盘从b杆移动到c杆，借助a杆。

而且这3步必须满足这样的先后顺序（其他的递归问题，子问题的求解顺序有可能运行变化）。

具体如何移动：

二 扩展问题(四根杆)

主要是记录下得出递归式的思考过程.

三根杆(A\B\C):

初始时n个圆盘全部有序(小的放在上面)的放在A杆上,把考虑重点放在第N号圆盘上,要把这个最大的圆盘从A杆移动到C杆,因为它最大,所以在移动的时候,C杆上面不能有任何圆盘,于是第1至n-1号圆盘都必须有序的放在B杆上,所以很容易就得出了递归式.

四根杆(A\B\C\D):

这时如果仍然把考虑重点放在第N号圆盘上,要把这个最大的圆盘从A杆移动到D杆,因为它最大,所以在移动的时候,D杆上面不能有任何圆盘,于是应该把第1至n-1号圆盘放在B杆和C杆上,但是放置方式多种多样,更加重要的是,子问题变成将n-1个圆盘放在B杆和C杆上,性质发生了变化,所以不能方便的得出递归式.

这时要找一个不同的思路,我们要将n个圆盘从A杆移动到D杆,可以先把第1-k号比较小的圆盘放在B杆上(这个是和四根杆hanoi性质一样的子问题),然后再把第k+1-n号比较大的圆盘从A杆移动到D杆(这个是和三根杆hanoi性质一样的子问题),最后把第1-k号圆盘从B杆移动到D杆(又是四根杆hanoi的子问题).这样就很容易得出的了递归式.

但是还有一个特别重要的问题:

为什么这种算法是完备的?为什么这种算法得出的结果一定是最优的?

这个算法目前并没有证明是最优的.能力有限,暂时也不多想了.