第二十九章：树的基本概念和性质

之前学习了数组、字符串、队列、栈等等数据类型和数据结构，它们都是线性存储结构。本章要学习的树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。

树结构不论是在竞赛中，还是在实际的工程开发中，都是一类重要的非线性数据结构，树中的节点之间具有明确的层次关系，并且每个节点会“分支”出若干个其他节点。

数据结构中的树和现实生活中的树长得一样，只不过我们习惯于处理问题的时候把树根放到上方来考虑。这种数据结构看起来像是一个倒挂的树，因此得名。后面我们提到的树均指数据结构中的树。

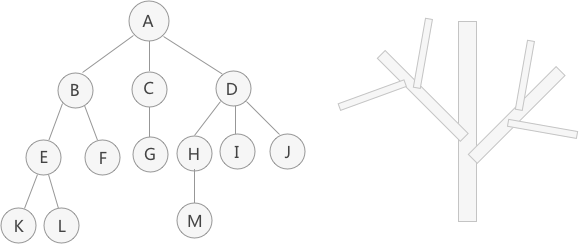
数据结构中的树和实际生活中的树的模型

学习目标：

1. 掌握树的相关的概念；
2. 掌握树的性质；
3. 对于具体问题，能够分析问题并判断问题中的数据能否用树结构表示。

一、树的定义

树的定义

树（Tree）是由 n(n≥0)n(n≥0) 个结点组成的一个非线性、具有层次关系的集合。（特别地，当 n = 0n=0 时，称树为空树，这是一种特殊情况）

树可以分为有根树和无根树两种：

• 有根树：有一个确定的根节点；
• 无根树：根不确定，任何结点都可以作为树的根；

无根树

无根树主要在后面将会学习的图论算法中的出现，不是现阶段学习的重点。

一个没有固定根结点的树称为无根树（unrooted tree）。无根树有几种等价的形式化定义：

• 有 nn 个结点， n-1n−1 条边的连通无向图
• 无向无环的连通图
• 任意两个结点之间有且仅有一条简单路径的无向图
• 任何边均为桥的连通图
• 没有圈，且在任意不同两点间添加一条边之后所得图含唯一的一个圈的图

无根树的例子也很多，例如 nn 个城市被 n-1n−1 条公里连在一起，如果将城市看作点，将公路看作边，那整个城市公路网络就是一棵树，因为没有明确的根结点，因此它是一棵无根树。