第六章 逻辑回归(Logistic Regression)(一)
第1节 分类和表示(Classification and Representation)
6.1 分类问题
参考视频:6 - 1 - Classification (8 min).mkv
在分类问题中,你要预测的变量 y y y是离散的,我们将学习一种叫做逻辑回归(Logistic Regression)的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。比如:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;区别一个肿瘤是恶性的还是良性的。
我们从二元的分类问题开始讨论:将因变量(dependant variable)可能属于的两个类 y y y分为 y = 0 y=0 y=0(负向类,负类,negative class)和 y = 1 y=1 y=1(正向类,正类,positive class),则因变量类 y ∈ { 0 , 1 } y\in\{0, 1\} y∈{0,1}。
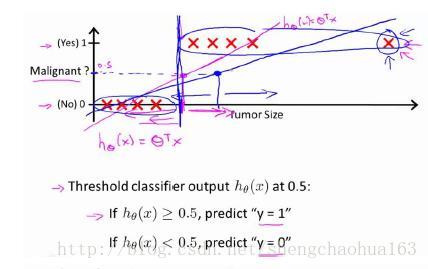
如上图,我们可以用线性回归算法来解决一个分类问题:当假设函数 h θ ( x ) ⩾ 0.5 h_{\theta}(x) \geqslant 0.5 hθ(x)⩾0.5,预测 y = 1 y=1 y=1,即正向类;当 h θ ( x ) ⩽ 0.5 h_{\theta}(x) \leqslant 0.5 hθ(x)⩽0.5,预测 y = 0 y=0 y=0,即负向类。但是,线性回归中假设函数的输出值可能远大于1或远小于0,这种输出值让人感觉很奇怪,要是所有的输出值能固定在0到1之间就好了。
我们接下来要研究的算法叫做逻辑回归算法,它的输出值永远在0到1之间,这个算法是监督学习的分类算法。
6.2 假说表示
参考视频 : 6 - 2 - Hypothesis Representation (7 min).mkv
本节展示假设函数的表达式,也就是说,在分类问题中,要用什么函数来表示我们的假设,这个函数的性质是它的输出值要在0和1之间。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在0和1之间。该模型的假设是:
h
θ
(
x
)
=
g
(
θ
T
x
)
h_{\theta}(x)=g(\theta^T x)
hθ(x)=g(θTx)其中
x
x
x代表特征向量,
g
g
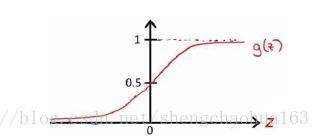
g代表逻辑函数(logistic function)。这是一个常用的逻辑函数S形函数(Sigmoid function),其公式为:
g
(
z
)
=
1
1
+
e
−
z
g(z) = \frac {1}{1+e^{-z}}
g(z)=1+e−z1。该函数图像如下:
合起来,我们得到逻辑回归模型的假设为: h θ ( x ) = 1 1 + e − θ T x h_{\theta}(x)=\frac {1}{1+e^{-\theta^T x}} hθ(x)=1+e−θTx1
h θ ( x ) h_{\theta}(x) hθ(x)的作用是:对于给定的输入变量,根据选择的参数计算出预测值 y = 1 y=1 y=1的可能性,即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_{\theta}(x)=P(y=1|x;\theta) hθ(x)=P(y=1∣x;θ), 1 − h θ ( x ) = P ( y = 0 ∣ x ; θ ) 1-h_{\theta}(x)=P(y=0|x;\theta) 1−hθ(x)=P(y=0∣x;θ)。例如,如果对于给定的 x x x,通过已经确定的参数计算出 h θ ( x ) = 0.7 h_{\theta}(x)=0.7 hθ(x)=0.7,则表示对于给定 x x x的预测值 y y y有70%的几率为正向类,30%的几率为负向类。这一点需要牢记!
6.3 判定边界
参考视频 : 6 - 3 - Decision Boundary (15 min).mkv
现在讲一下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
在逻辑回归中,我们预测:
- 当 h θ ⩾ 0.5 h_{\theta} \geqslant 0.5 hθ⩾0.5时,预测 y = 1 y=1 y=1
- 当 h θ < 0.5 h_{\theta} < 0.5 hθ<0.5时,预测 y = 0 y=0 y=0
根据上面绘制出的S形函数图像,我们知道:
- 当 z = 0 z=0 z=0时, g ( z ) = 0.5 g(z)=0.5 g(z)=0.5
- 当 z > 0 z>0 z>0时, g ( z ) > 0.5 g(z)>0.5 g(z)>0.5
- 当 z < 0 z<0 z<0时, g ( z ) < 0.5 g(z)<0.5 g(z)<0.5
又因为 z = θ T x z=\theta^T x z=θTx,即:
- θ T x \theta^T x θTx大于等于0,预测 y = 1 y=1 y=1(把等于0的情况归到正向类中)
- θ T x \theta^T x θTx小于0,预测 y = 0 y=0 y=0
现在假设我们有一个模型:并且参数
θ
\theta
θ是向量
[
−
3
1
1
]
[-3\ 1\ 1]
[−3 1 1],当
z
=
θ
T
x
=
−
3
+
x
1
+
x
2
z = \theta^T x = -3+x_1+x_2
z=θTx=−3+x1+x2 大于等于0,即
x
1
+
x
2
x_1+x_2
x1+x2大于等于3时,模型将被预测
y
=
1
y=1
y=1。
我们可以绘制直线
x
1
+
x
2
=
3
x_1+x_2=3
x1+x2=3,这条线便是我们模型的分界线,将预测为1的区域和预测为0的区域(正向类和负向类的区域)分隔开。如下图:
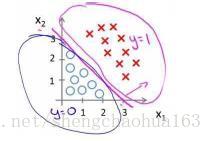
假使我们的数据呈现这样的分布情况,什么样的模型才适合呢?
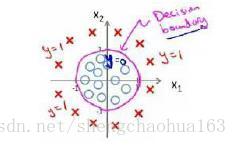
因为需要用曲线才能分隔 y = 0 y=0 y=0的区域和 y = 1 y=1 y=1的区域,我们需要二次方特征:模型为 h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) h_{\theta}(x)=g(\theta_0+\theta_1 x_1+\theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22),其中参数 θ = [ − 1 , 0 , 0 , 1 , 1 ] \theta=[-1,0,0,1,1] θ=[−1,0,0,1,1],则我们得到的边界恰好是圆心在原点半径为1的圆形。











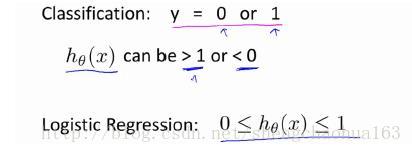

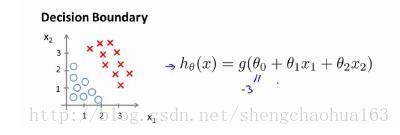















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








