小波的秘密1_小波变换概况与综述

1.有了Fourier，为什么还需要Wavelet?

先来揭揭短：

（1）Fourier分析不能刻画时间域上信号的局部特性。

（2）Fourier分析对突变和非平稳信号的效果不好，没有时频分析。

傅立叶变换将函数投影到正弦波上，将函数分解成了不同频率的正弦波，这不能不说是一个伟大的发现，但是在大量的应用中，傅立叶变换的局限性却日趋明显，事实上在光滑平稳信号的表示中，傅立叶基已经达到了近似最优表示，但是日常生活中的信号却并不是一直光滑的，而且奇异是平凡的，傅立叶在奇异点的表现就着实让人不爽，从方波的傅立叶逼近就可以看出来，用了大量不同频率的三角波去逼近其系数衰减程度相当缓慢，而且会产生Gibbs效应。其内在的原因是其基为全局性基，没有局部优化能力，以至局部一个小小的摆动也会影响全局的系数。实际应用中很需要时频局部化，傅立叶显然缺乏此能力了。即使如此，由于其鲜明的物理意义和快速计算，在很多场合仍然应用广泛。傅立叶变换在从连续到离散的情形是值得借鉴与学习的，大家都知道，时间周期对应频域离散，时间离散对应频域周期，时间离散周期对应频域离散周期，DFT其实是将离散信号做周期延拓然后做傅立叶变换再截取一个周期，反变换同样如此，所以DFT用的是块基的概念，这样如果信号两端的信号连接后不再光滑（即使两边都光滑），同样会在边界上产生大幅值系数（边界效应），延伸到图像中就是块效应。当对信号做对称周期延拓后再做傅立叶变换得到的正弦系数全部为0，也就是任何对称函数可以写成余弦的线性组合，同样按照离散的思路构造得到的是离散块余弦基，即DCT变换，虽然DCT可以通过对称后周期延拓再变换减少了边界效应（两边信号接上了，但不一定平滑），但也不能消除块效应，尤其是图像变换中人为将图像分成8*8处理后块效应更加明显。但是DCT很好的能量聚集效应让人惊奇，加之快速计算方法使它替代DFT成为图像的压缩的标准了很长时间（JPEG）。

闲扯了这么多，不要迷糊，开始上图：

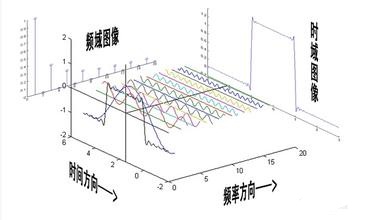
第一个就是傅立叶变换是整个时域，所以没有局部特征。这是由基函数决定的，同时如果在时域发生突变，那么在频域就需要大量的正弦波去拟合，这也是傅立叶变换性质决定的。

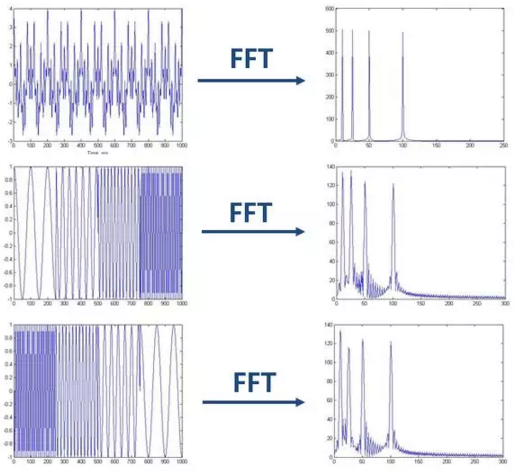
第二个就是面对非平稳信号，傅立叶变换可以看到由哪些频率组成，但不知道各成分对应的时刻是什么。也就是没有时频分析，看不出来信号频域随着时间变换的情况，反过来说就是，一个的频图对应好几个时域图，不知道是哪个，这个在实际应用中就不方便了，如图：