数据结构之堆

堆数据结构

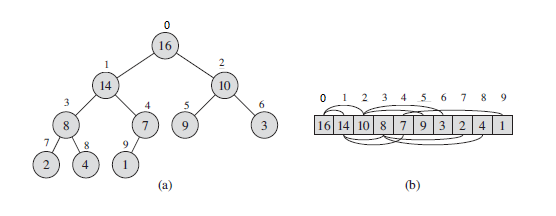
堆是一种特殊的数据结构，也可以称为优先级队列。堆可以近似的看成是一颗完全的二叉树。既可以使用链表实现也可以使用数组实现。但是使用数组实现比较方便。其使用数组实现的一个堆如下图所示。

堆可以分为最大堆和最小堆，堆具有一个非常重要的性质：
对于最大堆：父节点的值要比其两个子节点(如果存在)大。
对于最小堆：父节点的值要比其两个子节点(如果存在)小。
其数学表现形式为：
最大堆: $A[parent(i)] > A[i]$
最小堆: $A[parent(i) < A[i]$
其中parent(i)表示节点下标为i的父节点的下标。
因此，对于最大堆来说根节点是堆中元素最大的节点。

对于数组来说：父节点、左孩子 和右孩子的小标计算为：(注意：下标从0开始)

parent(i)
    return (i-1)/2;

left(i)
    return i*2 + 1;

right(i) 
    return (i+1)*2;

堆的操作：

堆的创建：创建一个堆。
因为使用数组来表示一个堆。因此，创建堆，就相当于创建一个数组。

插入操作：将元素插入到堆中，并且要保持堆的性质。
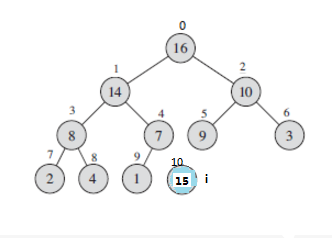
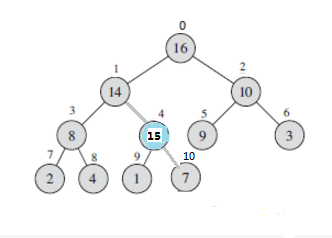
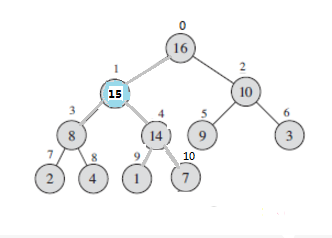
插入元素到堆中，首先我们将元素插入到数组最后一个元素的下一个位置(假设下标为i)，如果A[parent(i)] < A[i] 则交换A[parent(i)] 和 A[i]的值，并且使i = parent(i)。一直重复该过程直到i =0或者不等式不成立，如下图所示。将元素15插入到堆中

其伪代码为：

//将元素item插入到heap中, heap为最大堆
insert(heap, item) {
    int i = heap.size; // 堆的大小，或者说堆中元素的个数
    heap[i] = item;  // 将元素插入到堆的最后一个元素的下一个位置
    ++heap.size;  // 堆的大小加1
    while ( i > 0 && heap[parent(i)] < heap[i]) {
        swap(heap, i, parent(i));  //交换
        i = parent(i);
    }
}

堆的删除 : 删除根节点。
删除根节点元素。首先取出根节点元素进行保存，然后再把堆中最后一个元素放到根节点，删除最后一个元素，在调整堆。其伪代码为：

deleteFirst(heap) {
    item = heap[0];  // 取出根节点
    N = heap.size;   // 堆中元素的个数
    heap[0] = heap[N-1];  
    heap[N-1] = null;  --heap.size;
    i = 0;
    //调整堆
    while(i*2 < N) {
        lchild = left(i); rchild = right(i);
        max = lchild;
        if (rchild < N) {  // 左右孩子都存在
            max = Max(lchild, rchild);   //找出左右孩子中的最大值
        } 
        if (heap[i] < heap[max]) {
            swap(heap, i, max);
            i = max;
        } else 
            break;
    }
    return item;
}

其完整的Java代码为：

package Sort;

import java.util.Arrays;
import java.util.Comparator;
import java.util.Random;

import static java.lang.System.out;

/**
 * 堆
 */
public class Heap<T extends Comparable<T>> {

    private T [] arr;
    private int N = 0;
    private Comparator comparator = null;

    private void swap(T[] arr, int i, int j) {
        T tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    /**
     * 创建一个默认大小的堆，默认为最小堆
     */
    public Heap() {
        arr = (T[]) new Comparable[20];
    }

    /**
     * 创建一个初始容量为cap的堆，默认为最小堆
     *
     * @param cap 初始容量
     */
    public Heap(int cap) {
        arr = (T[]) new Comparable[cap];
    }

    /**
     * 比较器
     *
     * @param comparator
     */
    public Heap(Comparator comparator) {
        this();
        this.comparator = comparator;
    }

    /**
     * 获取堆的大小
     *
     * @return 堆的大小
     */
    public int size() {
        return N;
    }

    /**
     * 将堆的大小重新调整为max
     *
     * @param max 堆的大小
     */
    private void resize(int max) {
        T[] tmp = (T[]) new Comparable[max];
        // 将数组中的元素拷贝到数组tmp上去
        System.arraycopy(arr, 0, tmp, 0, N);
        arr = tmp;
    }

    /**
     * 判断堆是否为空
     *
     * @return 如果为空返回true，否则返回false
     */
    public boolean isEmpty() {
        return N == 0;
    }

    /**
     * 将元素插入到堆中
     *
     * @param item
     */
    public void insert(T item) {
        if (N == arr.length) resize(2 * N);
        int i = N;
        arr[i] = item;  //首先先将元素插入到堆的后面
        //调整堆
        while (i > 0) {
            if( (comparator != null && comparator.compare(arr[(i-1)/2], arr[i]) > 0)
                    || (comparator==null && arr[(i-1)/2].compareTo(arr[i]) > 0) ) {
                swap(arr, (i-1)/2, i);
                i = (i-1)/2;
            } else
                break;
        }
        ++N;
    }

    /**
     * 获取堆中的第一个元素
     * @return 如果堆存在元素则放回第一个元素，否者返回null
     */
    public T getFirst() {
        if (N > 0) return arr[0];
        else
            return null;
    }

    /**
     * 删除堆的第一个元素
     * @return 如果堆不为空则返回堆中第一个元素，否则返回null
     */
    public T deleteFirst() {
        T elem = null;
        if (N > 0) {
            elem = arr[0];
            arr[0] = arr[N-1];
            arr[N-1] = null; --N;
            // 调整堆
            int parent = 0, ch;
            while ((parent+1)*2 <= N) {
                ch = 2*parent + 1;  //左孩子
                //存在右孩子
                if ((ch + 1) < N ) {
                    // 找出左右孩子较小的结点
                    if ((comparator!=null && comparator.compare(arr[ch], arr[ch+1]) > 0 )
                            || (comparator==null && arr[ch].compareTo(arr[ch+1])>0)) {
                        ch = ch+1;
                    }
                }
                if ((comparator != null && comparator.compare(arr[parent], arr[ch]) > 0) ||
                        (comparator==null && arr[parent].compareTo(arr[ch]) > 0)) {
                    swap(arr, parent, ch);
                    parent = ch;
                } else
                    break;
            }
        }
        return elem;
    }
    public static void main(String [] args) {
        // 创建一个最大堆
        Heap<Integer> heap = new Heap<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer a, Integer b) {
                return Integer.compare(b, a);
            }
        });

        int [] arr = new int[30];
        Random random = new Random();
        for (int i = 0; i < arr.length; ++i) {
            arr[i] = random.nextInt(50);
            heap.insert(arr[i]);
        }
        Arrays.sort(arr);

        out.println(Arrays.toString(arr));
        while (!heap.isEmpty())
            out.print(heap.deleteFirst() + " ");
    }
}