【多项式n连】各种多项式模板（从入门到入土）

最新推荐文章于 2021-02-20 19:14:29 发布

_shivering_

最新推荐文章于 2021-02-20 19:14:29 发布

阅读量1.6k

点赞数 2

分类专栏：数学

本文链接：https://blog.csdn.net/shiveringkonnyaku/article/details/88073020

版权

qwq。。。好像很久没有写博客了的样子。。。因为最近一段时间一直处在觉得自己太蒻了的焦虑当中。。。导致啥也没学进去。。。这样的。。。本来定下的肝高数和概率论的计划也因为各种各样的原因没能完成。。。而降低到了只是零散地又复习了一些数学。。。然后发现luogu上有很多多项式的板子。。。就去做了一点。。。这样子。。。然后发现好久没更博客了。。。就准备放上来一些。。。也算是水一水博客了。。。反正老年选手已经半AFO了。。。。。。省选注定滚粗了。。。。已经到了结束的时候了吧。。。。。。好像也很突然呢。。。。可是这么蒻的话，难道不是早有预料的吗。。。orz。

然后蒟蒻是一个数学很不好的蒟蒻。。。如果dalao们发现错误的话希望可以指出一下。。。之类的。。。虽然应该不太会有人看到这篇写得很渣又很弱的博客。。。orz。

一、对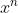 $x^n$ 取模

$A(x)\ mod\ x^n$ 相当于留下 $a_0,a_1,...,a_{n-1}$ ，把幂次>=n的项都截去。

二、加减

$A(x)-B(x)=\sum_{i=0} ^{n-1}\ a_i-b_i$ (其中n=max(A的项数，B的项数))。加法同理。这是O(n)的。

三、乘法

$A(x)*B(x)=\sum_{i=0}^{n-1}x^i\sum_{j=0}^{j=i}a[j]*b[i-j]$ 暴力计算是O(n^2)的。这里仅写如何O(n log n)计算。

前置：

复数基础

i=sqrt(-1)，记一个复数为a+bi，将它用直角坐标系表示，则它的坐标为(a,b)。这样的坐标系称为复平面。

每个复数与复平面上的点一一对应。

记复平面上点(x,y)与原点的连线与x轴正半轴的夹角为它的辐角，连线的长度为它的模长。

复数的四则运算：

加法：(a1+i*b1)+(a2+i*b2)=(a1+a2)+i*(b1+b2) 减法同理。

乘法：(a1+i*b1)*(a2+i*b2)=(a1*a2-b1*b2)+i*(a1*b2+a2*b1)

除法：(a1+i*b1)/(a2+i*b2)=(a1+i*b1)*(a2-i*b2)/(a2*a2+b2*b2)

记复数a+bi的共轭复数为a-bi，那么除以一个复数就等于上下同乘它的共轭复数。

其中，复数的乘法运算的几何意义相当于辐角相加，模长相乘（这两者同时确定时，一个复数也就被唯一确定了）。

证明：模长相乘很显然，不写了。

$(\cos\ \alpha_1+i*\sin\ \alpha_1)*(\cos\ \alpha_2+i*\sin\ \alpha_2)\\ =(\cos\ \alpha_1 * \cos\ \alpha_2-\sin\ \alpha_1*\sin\ \alpha_2) +i*(\cos\ \alpha_2 * \sin\ \alpha_1+\cos\ \alpha_1 *\sin\ \alpha_2)\\ =\cos(\alpha_1+\alpha_2)+i*\sin(\alpha_1+\alpha_2)$

而辐角相加就是基础的三角函数运用，推导如上。具体内容见高中数学必修课本。

单位根：

如果在复平面上画一个单位圆，用从原点出发的射线把这个圆n等分，那么与x轴正半轴夹角为正且夹角最小的那条射线与圆的交点坐标是 $(\cos(\frac{2\pi}{n}),\sin(\frac{2\pi}{n}))$ ，将它对应的复数记作n等分下的单位根 $\omega_n$ 。（事实上，单位根就是n次幂为1的复数）根据复数的乘法法则，单位根的k次方正好是从x轴正半轴往上数k个1/n的点（单位圆上的复数模长都是1，故只要辐角相加），记作 $\omega_n^k$ 。

于是：有 $\omega_n^k=-\omega_n^{k+n/2}$ ， $\omega_n^k=\omega^{k+n}_n$ ， $\omega_{k}^{n}=\omega_{k/2}^{n/2}$ 。

FFT（Fast Fourier Transform，快速傅里叶变换）：

多项式的乘法其实是一种卷积，而当我们采用系数表示法时，这种卷积的优化空间已经不大了。

因此，我们采用点值表示法。可以证明，用n组线性无关的向量(xi,yi)能唯一确定一个n-1次多项式。其中yi是将xi带入该多项式内得到的值。于是，只要得到多项式在这样n个xi上的取值，就可以用这些(xi,yi)表示它（求值可以暴力O(n^2))。当然，知道了n对这样的(xi,yi)，也可以反推出原本的多项式（虽然有些麻烦，但是显然可以暴力用O(n^3)的高斯消元）。并且，对多项式进行加减乘除，则相当于它的点值也对应地加减乘除了。而求点值与逆推过去这两个过程的优化空间就很大了，因为我们可以自选一些具有特殊性质的xi，使它能够被一些算法所优化。事实上，FFT算法就是选择了xi= $\omega_n^i$ ，利用了单位根的特殊性质，然后分治优化成O(n log n)的。

现在假设要求多项式A(x)在x= $\omega_n^0,\omega_n^1,...,\omega_n^{n-1}$ 处的取值，并且n是2的整数次幂（如果实际不到，可以在高位补0）。

（从多项式的系数表示推出其点值表示的过程被称为DFT）

那么把A(x)分成两个长度为n/2的多项式，A_0(x)与A_1(x)，其中A_0(x)每项的系数按照顺序分别对应着A(x)每个偶次项的系数，A_1(x)则对应着每个奇次项。（这也就是为什么要让n是2的整数次幂，这样可以确保每次都等分了n）即：

$A_0(x)=a_0*x^0+a_2*x^1+...+a_{n-2}*x^{n/2-1} =\sum_{i=0}^{n/2-1}a_{2i}*x^i \\ A_1(x)=a_1*x^0+a_3*x^1+...+a_{n-1}*x^{n/2-1} =\sum_{i=0}^{n/2-1}a_{2i+1}*x^i$

然后递归下去，分别求出A_0(x)和A_1(x)在x=

最低0.47元/天解锁文章

_shivering_

关注

2
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
【多项式n连】各种多项式模板（从入门到入土）

qwq。。。好像很久没有写博客了的样子。。。因为最近一段时间一直处在觉得自己太蒻了的焦虑当中。。。导致啥也没学进去。。。这样的。。。本来定下的肝高数和概率论的计划也因为各种各样的原因没能完成。。。而降低到了只是零散地又复习了一些数学。。。然后发现luogu上有很多多项式的板子。。。就去做了一点。。。这样子。。。然后发现好久没更博客了。。。就准备放上来一些。。。也算是水一水博客了。。。反正老年选手已...
复制链接

扫一扫