从零实现机器学习算法（十九）高斯混合模型-CSDN博客

本文链接：https://blog.csdn.net/sinat_35821976/article/details/118075106

01. 高斯混合模型简介

高斯混合模型（Gaussian Mixed Model，GMM）和隐马尔可夫模型(Hidden Markov Model, HMM)是语音算法中常用的统计模型。HMM前面已经讲过了，这里介绍一下GMM算法。当数据分布中有多个峰值的时候，如果使用单峰分布函数去拟合会导致结果不佳，这时候可以使用具有多个峰值的分布去拟合，如下图所示，可以明显的看到使用两个峰值的高斯模型比单个峰值的高斯模型能更好的拟合数据。

GMM同K-means算法一样也使用了EM算法进行迭代计算。GMM假设每个簇的数据都是符合高斯分布的，当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果，即

其中

02 高斯混合模型

一般情况下我们不能直接求解GMM的参数，而是在观察一系列数据的基础之上给出类别数量K，希望求得最佳的K个高斯分模型。此时问题转化为最佳的K个高斯模型的均值μ，方差σ、以及混合权重α的求解。这类问题通常通过最大似然估计来求解。遗憾的是，高斯混合模型中如果直接使用最大似然估计将会得到一个复杂的非凸函数，目标函数是和的对数，难以展开和对其求偏导。因此我们使用EM算法来逐渐逼近最优解。EM算法原理在前面的机器学习文章中已经讲过很多了这里就不再赘述了。我们假设观测变量yj中来自第个模型的分量为隐变量，记为γjk。γjk是第j个观测数据来自第k个模型的概率，被称第k个分模型对观测数据yj的响应度并且满足

其中N为样本数目，K为分模型的数目。此时对数似然函数可以写为

在EM算法中的E步，求Q函数

其中

在EM算法中的M步，极大化Q函数

并且分别对μk, σk,αk求偏导，并令偏导等于0，可以求得

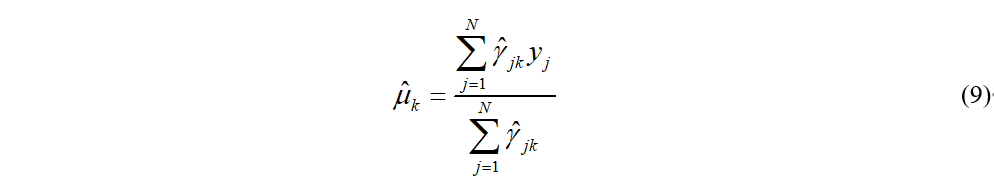
不断重复E步和M步直到对数似然函数收敛即完成训练。无监督对应代码如下：

    def train(self, train_data, plotResult=True):        self.N = len(train_data)        self.gamma = np.zeros([self.N, self.K])        for i in tqdm(range(self.iterations)):            # E-step            for k in range(self.K):                self.gamma[:,k] = self.GaussianPDF(self.mu[k], self.sigma[k], train_data)            for j in range(self.N):                self.gamma[j,:] = self.gamma[j,:] / np.sum(self.gamma[j,:])            # M-step            for k in range(self.K):                gamma_sum = np.sum(self.gamma[:,k])                self.mu[k] = np.sum(np.dot(self.gamma[None,:, k], train_data), axis=0) / gamma_sum                self.sigma[k] = (train_data - self.mu[k]).T * np.multiply(np.mat(train_data - self.mu[k]), np.mat(self.gamma[:, k]).T) / gamma_sum                self.alpha[k] = gamma_sum / self.N        self.label = np.argmax(self.gamma, axis=1)        if plotResult:            self.plotResult(train_data)        return self.label