Codeforces Round #140 (Div. 2) A. Where do I Turn?

A. Where do I Turn?

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Trouble came from the overseas lands: a three-headed dragon Gorynych arrived. The dragon settled at point C and began to terrorize the residents of the surrounding villages.

A brave hero decided to put an end to the dragon. He moved from point A to fight with Gorynych. The hero rode from point A along a straight road and met point B on his way. The hero knows that in this land for every pair of roads it is true that they are either parallel to each other, or lie on a straight line, or are perpendicular to each other. He also knows well that points B and C are connected by a road. So the hero must either turn 90 degrees to the left or continue riding straight ahead or turn 90 degrees to the right. But he forgot where the point C is located.

Fortunately, a Brave Falcon flew right by. It can see all three points from the sky. The hero asked him what way to go to get to the dragon's lair.

If you have not got it, you are the falcon. Help the hero and tell him how to get him to point C: turn left, go straight or turn right.

At this moment the hero is believed to stand at point B, turning his back to point A.

Input

The first input line contains two space-separated integers x_a, y_a (|x_a|, |y_a| ≤ 10⁹) — the coordinates of point A. The second line contains the coordinates of point B in the same form, the third line contains the coordinates of point C.

It is guaranteed that all points are pairwise different. It is also guaranteed that either point B lies on segment AC, or angle ABC is right.

Output

Print a single line. If a hero must turn left, print "LEFT" (without the quotes); If he must go straight ahead, print "TOWARDS" (without the quotes); if he should turn right, print "RIGHT" (without the quotes).

Examples

Input

Copy

0 0
0 1
1 1

Output

Copy

RIGHT

Input

Copy

-1 -1
-3 -3
-4 -4

Output

Copy

TOWARDS

Input

Copy

-4 -6
-3 -7
-2 -6

Output

Copy

LEFT

Note

The picture to the first sample:

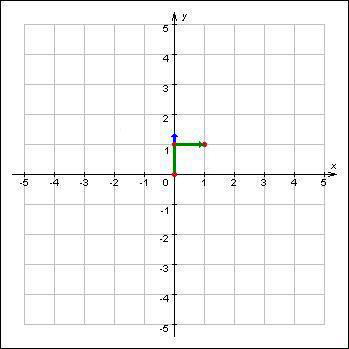
The red color shows points A, B and C. The blue arrow shows the hero's direction. The green color shows the hero's trajectory.

The picture to the second sample:

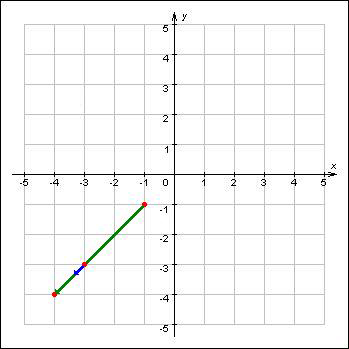
思路：

咋一看貌似很复杂，其实很简单。运用数学知识，很容易就可以解决。这里主要运用的就是向量的叉乘。

假的A(xa,ya),B(xb,yb),C(xc,yc)那么向量BA（xa-xb，ya-yb）;BC(xc-xb,yc-yb)

两个向量叉积的模计算如下

BA×BC=|BA||BC|sin(θ)

BC×BA=|BC||BA|sin(φ)

即夹角是第二个向量到第一个向量的顺时针方向的夹角，或者说第一个向量到第二个向量的逆时针方向的夹角。

 

当BA×BC的值大于0时说明BA为BC顺时针转过90度，对应RIGHT

当BA×BC的值小于0时说明BA为BC逆时针转过90度，对应LEFT

当BA×BC的值等于0时说明BA为BC顺时针转过180度。对应TOWARDS

BA×BC=(x1,y1)×(x2,y2)=下面的行列式

|x1 y1|

|x2 y2|

=x1*y2-x2*y1。

于是就可以根据结果输出答案

代码也是超级简单：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <cmath>
#include <map>
#define pi acos(-1.0)
#define ll long long
using namespace std;

int main(){
    ll xa,ya;
    ll xb,yb;
    ll xc,yc;
    cin>>xa>>ya;
    cin>>xb>>yb;
    cin>>xc>>yc;
    ll ans=(xa-xb)*(yc-yb)-(ya-yb)*(xc-xb);
    if(ans>0) cout<<"RIGHT"<<endl;
    else if(ans<0) cout<<"LEFT"<<endl;
    else cout<<"TOWARDS"<<endl;
    return 0;
}