leetcode 363. Max Sum of Rectangle No Larger Than K | 363. 矩形区域不超过 K 的最大数值和（前缀和，图文详解）-CSDN博客

本文链接：https://blog.csdn.net/sinat_42483341/article/details/118460992

该博客详细介绍了如何利用前缀和和容斥原理来解决LeetCode上的一个问题——找到矩阵中和不超过K的最大子矩阵。博主首先建立了横向和纵向的累加和数组，并通过双重循环计算所有可能的子矩阵，通过容斥原理求得最大和。最终，代码返回了最大和并处理了特殊情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

https://leetcode.com/problems/max-sum-of-rectangle-no-larger-than-k/
在这里插入图片描述

题解

本题利用 前缀和 的思想。

首先，分别建立横向、纵向辅助数组 rowSum[][], colSum[][]。其中：

横向辅助数组 看作是一维的，每行的 rowSum[i] 第表示的是从 0 到 i 的累加和；
纵向辅助数组 看作是二维的，每列均由 rowSum 纵向遍历相加所得，colSum[i][j] 表示的是从 [0,0] 位置 到 [i,j] 位置 的矩阵的累加和，表示面积。

然后，根据容斥原理：
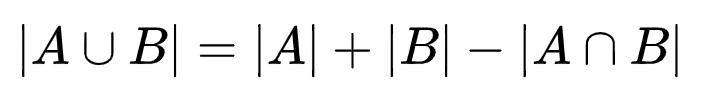
在这里插入图片描述
便可以得到如下图所示的思路。

在这里插入图片描述
直接上代码：

class Solution {
    public int maxSumSubmatrix(int[][] matrix, int k) {
        int M = matrix.length;
        int N = matrix[0].length;
        // 横向累加和
        int[][] rowSum = new int[M][N + 1];
        for (int i = 0; i < M; i++) {
            rowSum[i][0] = 0;
            for (int j = 1; j < N + 1; j++) {
                rowSum[i][j] = rowSum[i][j - 1] + matrix[i][j - 1];
            }
        }

        // 纵向累加和（面积）
        int[][] colSum = new int[M + 1][N + 1]; // 第1行 第1列 均为0
        for (int i = 0; i < N + 1; i++) {
            colSum[0][i] = 0;
            for (int j = 1; j < M + 1; j++) {
                colSum[j][i] = colSum[j - 1][i] + rowSum[j - 1][i];
            }
        }

        // 容斥原理
        int result = Integer.MIN_VALUE;
        for (int x1 = 1; x1 < M + 1; x1++) {
            for (int y1 = 1; y1 < N + 1; y1++) {
                for (int x2 = x1; x2 < M + 1; x2++) {
                    for (int y2 = y1; y2 < N + 1; y2++) {
                        int s = colSum[x2][y2] - colSum[x1 - 1][y2] - colSum[x2][y1 - 1] + colSum[x1 - 1][y1 - 1];
                        if (s == k) return k;
                        else if (s < k) result = Math.max(result, s);
                    }
                }
            }
        }
        return result;
    }
}

在这里插入图片描述