leetcode 523. Continuous Subarray Sum | 523. 连续的子数组和（同余定理）

寒泉Hq

于 2021-09-22 09:07:30 发布

阅读量4.8w

点赞数

分类专栏： LeetCode 文章标签： leetcode 算法 python

本文链接：https://blog.csdn.net/sinat_42483341/article/details/120408597

版权

LeetCode 专栏收录该内容

377 篇文章

订阅专栏

本文提供了一种解决LeetCode上连续子数组和问题的有效方法，采用O(n)的时间复杂度。通过使用前缀和及哈希映射记录前缀和的余数来快速判断是否存在满足条件的连续子数组。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

https://leetcode.com/problems/continuous-subarray-sum/
在这里插入图片描述

题解

没有想到 O(n) 的方法，于是直奔答案：

参考1：【宫水三叶】拓展到求方案数问题
参考2：证明+动图：帮你吃透本题

核心思想：
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

草稿：

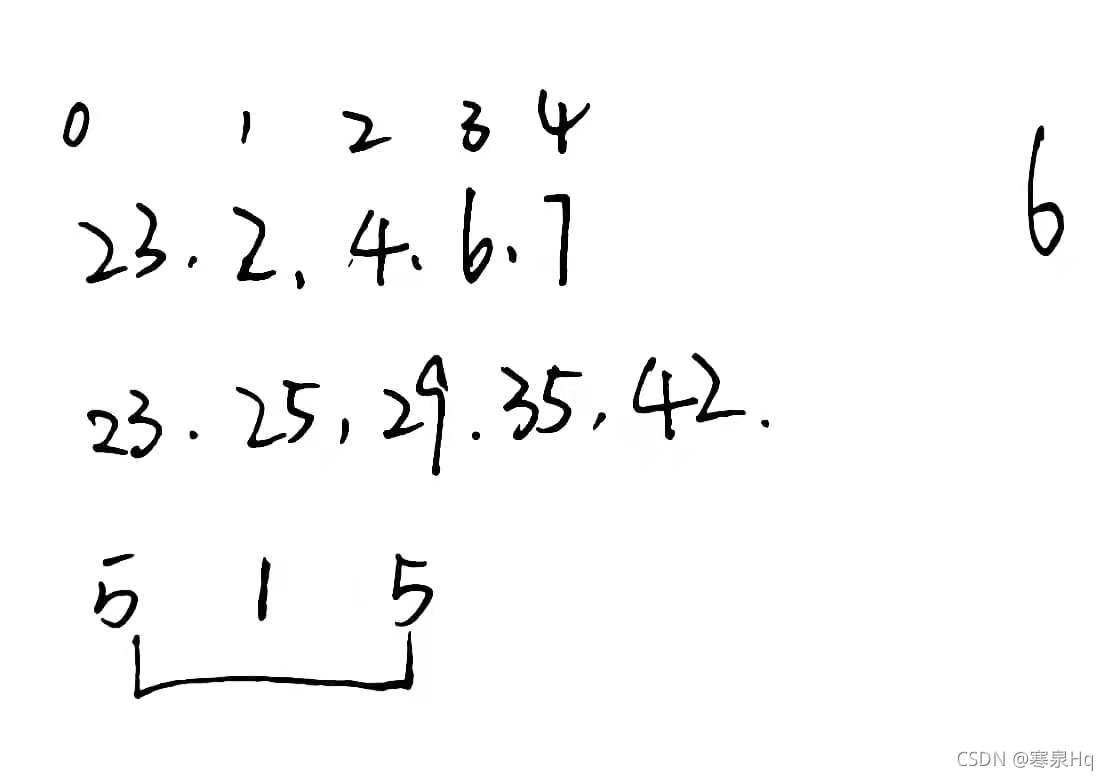
class Solution {
    public boolean checkSubarraySum(int[] nums, int k) {
        int[] sum = new int[nums.length];
        sum[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            sum[i] = sum[i - 1] + nums[i];
        }
        HashMap<Integer, Integer> map = new HashMap<>(); // (从0开始的前缀和%k，对应的结束下标)
        map.put(0, -1); // e.g. nums=[2,4,7]
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(sum[i] % k)) {
                if (i - map.get(sum[i] % k) >= 2) return true;
            } else {
                map.put(sum[i] % k, i);
            }
        }
        return false;
    }
}

在这里插入图片描述