最长问题记录

1、最长回文字符串
例子：如”isabba” 、”abcbaXXab” 这样子的字符串，部分是回文的，求出最长的回文部分。

解法一思路：
穷尽字符串。将字符串拆分成子字符串，然后对子字符串进行回文判断，并记录其长度。

 public static void main(String[] args){
        String str = "isabbaXXab";
        int len = str.length();
        int maxLen = 0;
        String maxStr = "";
        for(int i = 0 ; i < len; i++){
            for(int j = i ; j <= len ; j++){
                if(isParm(str.substring(i,j))){
                    if(j - i > maxLen){
                        maxLen = j - i;
                        maxStr = str.substring(i,j);
                    }
                }

            }
        }
        System.out.println(maxLen);
        System.out.println(maxStr);

    }

    public static boolean isParm(String str){
        int len = str.length();
        for(int i = 0 ; i < len / 2; i++){
            if(str.charAt(i) != str.charAt(len - i - 1)){
                return false;
            }
        }
        return true;
    }

解法二：动态规划【本人是垃圾还没参透，参透了再记录】

---

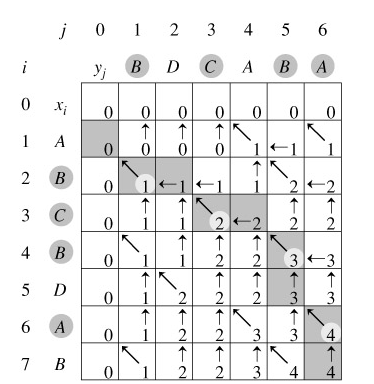
2、有删除情况下的最长回文字符串

解题思路：

这个题严格意义上来说，删除了字符就谈不上回文串了，既然有删除，那估计考察的不是回文串，而是其他的，但是这个东西又有回文串的特点，细想一下——那就是不连续的回文串，想到不连续，就容易使人想到最长公共子序列，把源字符串逆序之后对比两个字符串发现：我靠，这不就是求两个序列的最长公共子序列（好像跟回文串没多大关系）。

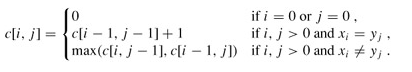
考察：回文串，动态规划，知识迁移

int dpLCS[M][M]; //设置成全局变量，自动初始化为0

//动态规划法:最长回文子串，有删除，其实就是求最长公共子序列
int LongestCommonSequence(string str)
{
    size_t n = str.size();
    if (n == 0 || n == 1)
        return 1;

    string s = str;
    reverse(s.begin(), s.end());

    for (size_t i = 1; i <= n; ++ i) {
        for (size_t j = 1; j <= n; ++ j) {
            if (str[i-1] == s[j-1]) 
                dpLCS[i][j] = dpLCS[i-1][j-1] + 1;
            else 
                dpLCS[i][j] = max(dpLCS[i-1][j], dpLCS[i][j-1]); 
        }
    }
    return dpLCS[n][n];
}

本段转自：http://www.cnblogs.com/bakari/p/5358257.html
http://blog.csdn.net/biangren/article/details/8038605

---

3、数组内连续升序的最长个数
例子：如｛5,3,4,7,2,9｝，3，4，7便是最长连续升序的。用动态规划来解决很简单。用一个dp[]来记录连续个数，通过比较每一个元素和之前的一个值的大小实现。

 public static void main(String[] args){
     int[] arr = {5,3,4,7,2,9};
     int length = arr.length;
     int[] dp = new int[length];
     dp[0] = 1;
     for(int i = 1; i < length; i++){
         if(arr[i] > arr[i-1]){
             dp[i] = dp[i-1]+1;
         } else {
             dp[i] = 1;
         }
    }
     int max = 0;
     for(int i = 0; i < length; i++){
         if(max < dp[i]){
             max = dp[i];
         }
     }
     System.out.print(max);
 }