树和二叉树概念及常见题型总结＜选择＞_度为m的哈夫曼树是什么意思-CSDN博客

本文链接：https://blog.csdn.net/six23333/article/details/120311160

本文探讨了树的基本性质，包括度为m的树和二叉树的特殊类型如满二叉树、完全二叉树和平衡二叉树。深入解析了结点个数问题，如计算叶节点、根据度分布求结点总数，并涉及完全二叉树的几种常见求解方法。此外，文章还涵盖了二叉树遍历、线索二叉树、哈夫曼树构造及其编码知识。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

一、树的四个性质
关于度为m树和 m叉树的
二、二叉树的相关
特殊二叉树
二叉树性质
三、结点个数问题
四、二叉树的几个遍历
几种特别的
线索二叉树相关
- 几种需要三叉链表才能求的
树、森林、二叉树相互转换
哈夫曼树、哈夫曼编码

一、树的四个性质

1.树中的结点数等于所有结点的度数加1

2.度为m的树中第i层最多的结点个数
在这里插入图片描述
（想要第i层结点最多，就说明i的上一层也要最多，当每一层的结点的度都是m时，取到最大值。例如度为2的树，第一层为1，第二层最多为2，第三层为4…)

3.高度为h的m叉树最多有结点个数
在这里插入图片描述
首项为1，公比为m，项数为h的等比数列求和

4.具有n个结点的m叉树的最小高度为

n的大小应该大于前h-1层的结点，小于前h层的最多结点
在这里插入图片描述

关于度为m树和 m叉树的

度为m的树说明至少有个结点的度为m，
但m叉树可以是空树。

二、二叉树的相关

特殊二叉树

满二叉树

高度为h ，含有结点数为
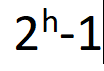
在这里插入图片描述
除叶结点外每个结点的度为2

完全二叉树

从左到右排序，在同一层不可能出现没有左结点而单独出现右结点的存在

在这里插入图片描述
第一个为完全二叉树，而第二个并非完全二叉树

二叉排序树

特点：结点的左孩子比他小，结点的右孩子比他大（左小右大）

在这里插入图片描述

平衡二叉树

平衡二叉树及它的翻转问题
.

二叉树性质

n0 = n2 + 1
推导： n = n0 + n1 + n2 = 1 + n1 + 2n2 ----> n0 = n2 + 1
第k层最多的结点数是

三、结点个数问题

1.已知各个度的结点个数，求它的叶结点个数

两个公式

n = n0 + n1 + n2 +…nm (n 为结点个数，m为最大度数）
n = 总分支数 + 1 = 1 + 1n1 + 2n2 + 3n3…

经典例题

在一棵度为4的树T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树T的叶结点个数是：
n = n0 +10 + 1 + 10 + 20 = 1 + 20*4 + 10 *3 + 1 *2 + 10 *1 > n0 = 123 - 41 = 81 个叶结点

关于完全二叉树求它的结点个数

例题类型1：已知总结点个数求叶结点

若一棵完全二叉树有768个结点，则该二叉树中叶结点个数是
思路一：最后一层的结点数加上倒数第二层的叶结点个数（若有）
可以得知前九层的总和为 512 - 1 = 511，
得出最后一层叶结点个数 768 - 511 = 257
但倒数第二层应有 2 的八次 = 256 个结点，若都不是叶结点至少在最后一层产生 256 * 2 = 512 个结点，但现在只有 257 ，257 / 2 = 128.5
至少由129 个上一层的结点产生
在上一层总个数 256-129 = 127 得出上一层叶结点个数；
127 + 257 = 384 为总共个数
思路二：由最后一个分支序号：总结点数除二取下限 768/2 = 384
768 - 384 = 384；