1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree(Leetcode每日一题-2021.01.21)--抄答案

本文链接：https://blog.csdn.net/sjt19910311/article/details/112971275

这篇博客介绍了如何找到一个加权无向连通图中最小生成树(MST)的临界边和伪临界边。临界边是指删除它会导致MST总权重增加的边，而伪临界边可能出现在某些MST中但不是所有。给定节点数n和带权重的边，博主分析了如何在满足所有节点连接且无环的情况下找到这些边。例子和解决方案也包含在内。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Problem

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional and weighted edge between nodes ai and bi. A minimum spanning tree (MST) is a subset of the graph’s edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph’s minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

Constraints:

2 <= n <= 100
1 <= edges.length <= min(200, n * (n - 1) / 2)
edges[i].length == 3
0 <= ai < bi < n
1 <= weighti <= 1000
All pairs (ai, bi) are distinct.

Example1

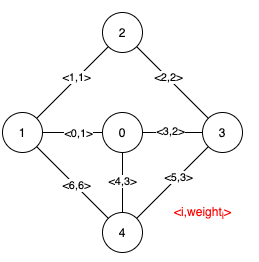
在这里插入图片描述

Example2

在这里插入图片描述
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

Solution

// 并查集模板
class UnionFind {
public:
    vector<int> parent;
    vector<int> size;
    int n;
    // 当前连通分量数目
    int setCount;
    
public:
    UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
        iota(parent.begin(), parent.end(), 0);
    }
    
    int findset(int x) {
        return parent[x] == x ? x : parent[x] = findset(parent[x]);
    }
    
    bool unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            swap(x, y);
        }
        parent[y] = x;
        size[x] += size[y];
        --setCount;
        return true;
    }
    
    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
};

class Solution {
public:
    vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {
        int m = edges.size();
        for (int i = 0; i < m; ++i) {
            edges[i].push_back(i);
        }
        sort(edges.begin(), edges.end(), [](const auto& u, const auto& v) {
            return u[2] < v[2];
        });

        // 计算 value
        UnionFind uf_std(n);
        int value = 0;
        for (int i = 0; i < m; ++i) {
            if (uf_std.unite(edges[i][0], edges[i][1])) {
                value += edges[i][2];
            }
        }

        vector<vector<int>> ans(2);
        
        for (int i = 0; i < m; ++i) {
            // 判断是否是关键边
            UnionFind uf(n);
            int v = 0;
            for (int j = 0; j < m; ++j) {
                if (i != j && uf.unite(edges[j][0], edges[j][1])) {
                    v += edges[j][2];
                }
            }
            if (uf.setCount != 1 || (uf.setCount == 1 && v > value)) {
                ans[0].push_back(edges[i][3]);
                continue;
            }

            // 判断是否是伪关键边
            uf = UnionFind(n);
            uf.unite(edges[i][0], edges[i][1]);
            v = edges[i][2];
            for (int j = 0; j < m; ++j) {
                if (i != j && uf.unite(edges[j][0], edges[j][1])) {
                    v += edges[j][2];
                }
            }
            if (v == value) {
                ans[1].push_back(edges[i][3]);
            }
        }
      
        return ans;
    }
};

//作者：LeetCode-Solution
//链接：https://leetcode-cn.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/solution/zhao-dao-zui-xiao-sheng-cheng-shu-li-de-gu57q/