P11079 「FSLOI Round I」山峦（AC代码）

P11079 「FSLOI Round I」山峦

题目背景

English statement. You must submit your code at the Chinese version of the statement.

山峦是造物主弃的酒杯。

题目描述

如果一个长度至少为三的序列 a 满足以下条件，则称其为一个山峰：

• 设其长度为 m。存在一个 x，满足 2≤x≤m−1，并且使得 a1​,a2​,⋯,ax​ 严格单调递增，ax​,ax+1​,⋯,am​ 严格单调递减。

特别地，称 ��ax​ 为这个山峰的高度。

如果一个序列 �b 满足以下任一条件，则称其为一个山峦：

• �b 序列是一个山峰。

• 可以拆成至少两个连续的子序列，使得每个子序列都是山峰，且从左到右山峰的高度严格单调递增。

比如，序列 {2,4,3,1,5,2,1} 是山峦，因为其可以拆分为 {2,4,3},{1,5,2,1} 两个山峰，且山峰高度严格递增。而序列 {2,4,3,5,2,1} 不是山峦，因为其无法拆分成至少两个连续的子序列，使得每个子序列都是山峰。

现在给定一个长度为 n 的序列 a，小 F 想知道，在 a 的所有子序列中，有多少个是山峦。由于答案可能很大，请输出其对 998244353 取余后的结果。

请注意，在本题中，即使子序列的元素相同，只要子序列的元素在 a 中的位置不同，仍算作不同的子序列。

输入格式

共两行。

第一行一个整数 n，表示序列长度。

第二行 n 个整数 a1​,a2​,⋯,an​，表示 a 序列。

输出格式

共一行。

一个整数，表示是山峦的子序列数量对 998244353 取余的结果。

输入输出样例

输入 #1

4
1 2 2 1

输出 #1

2

输入 #2

7
2 4 3 1 5 2 1

输出 #2

35

输入 #3

20
2 3 5 6 8 7 6 5 6 7 8 8 8 8 4 3 5 6 7 4

输出 #3

15085

说明/提示

【样例 1 解释】

由 a1​,a2​,a4​ 构成的子序列是山峦，由 a1​,a3​,a4​ 构成的子序列是山峦。

【数据规模与约定】

本题采用捆绑测试。

对于 100% 的数据，保证：

• 1≤≤500
• 1≤≤

子任务	分值	特殊性质
1	10	n≤18
2	15	n≤80
3	15	A
4	20	B
5	40	无

特殊性质 A：序列 a 是山峰。

特殊性质 B：序列 a 中的元素互不相同。

---

【题解】

考虑 DP，设 ​ 为在第 i 个点结束的山峦子序列，其中最右边的一座山峰的山顶高度是 j，现在构成的形状形如 k 的，方案数量。其中 k∈[0,5]，对应的形状如图所示：

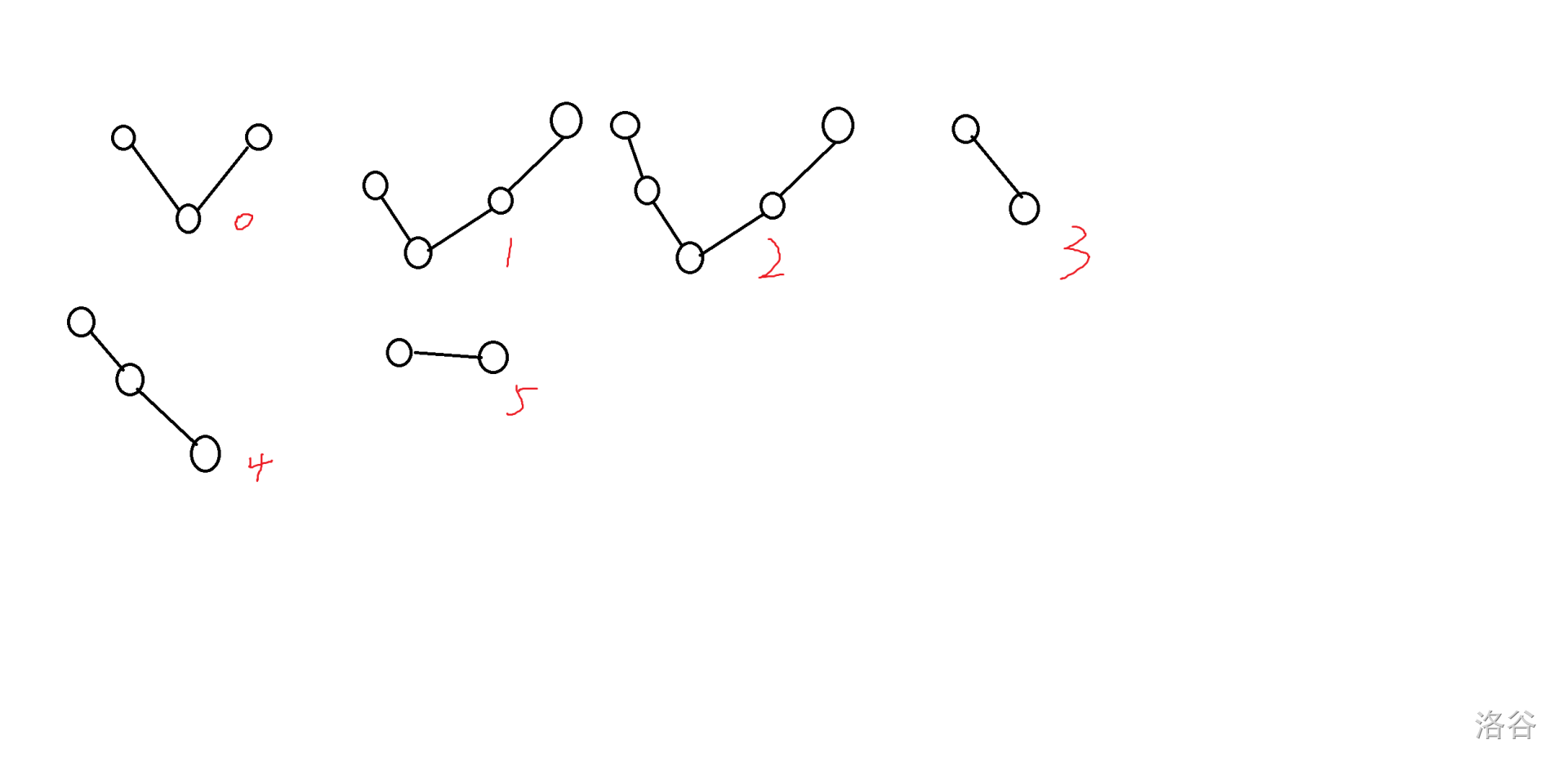
这里解释一下以上 6 种情况。

第 0 种，由山顶向下走了一格，然后往上走一格。

第 1 种，由山顶向下走了一格，然后向上走了两格以上。

第 2 种，由山顶向下走了两格以上，然后向上走了两格以上。

第 3 种，由山顶向下走了一格，

第 4 种，由山顶向下走了两格以上。

第 5 种，平着走了一格。

接下来考虑状态之间如何转移。

因为从山顶往下走一格之后往上走，若再往下走一格，就不能形成两座并列的山峰了，因为这样它们的一个端点会重合，所以第 0 种情况后，只能往上走。

第 5 种情况也一样，山峰右边是严格递减，左边严格递增，出现两个相邻的相等的数，那一定是一个属于左边那座山的右端点，一个属于右边那座山的左端点。

发现第二维的值域达到了 106，考虑离散化，于是降到 5×102。

最后考虑统计答案，为了形成山峦，序列最右边一定是一座山峰的下降部分，因此  ，其中 p 表示离散化后的值域。

设值域 p 与 n 同阶，则时间复杂度为 O()。

【代码】

#include <bits/stdc++.h>
using namespace std;

#define int long long

#define endl '\n'
#define FRR(file) freopen(file,"r",stdin)
#define FRW(file) freopen(file,"w",stdout)
#define _rep(i,a,b) for (int i=(a);i<=(b);++i)
#define _reps(i,a,b,c) for (int i=(a);i<=(b);c)
#define _rrep(i,a,b) for (int i=(a);i>=(b);--i)
#define _rreps(i,a,b,c) for (int i=(a);i>=(b);c)
#define _iter(i,a) for (auto i=a.begin();i!=a.end();++i)
#define _graph(i,u) for (int i=h[u];~i;i=ne[i])
#define rint register int
#define LL long long
typedef pair<int,int> pii;

const int N=505;
const int mod=998244353;

int n;
int arr[N];
int f[N][N][6];
vector<int> nums;
int p;
bool cmp(const int& a,const int& b) {
    return a<b;
}
signed main() {
    scanf("%lld",&n);
    _rep(i,1,n) scanf("%lld",&arr[i]);
    _rep(i,1,n) nums.emplace_back(arr[i]);
    sort(nums.begin(),nums.end(),cmp);
    nums.erase(unique(nums.begin(),nums.end()),nums.end());
    p=nums.size()-1;
    _rep(i,1,n) arr[i]=lower_bound(nums.begin(),nums.end(),arr[i])-nums.begin();
    _rep(i,1,n) {
        f[i][0][0]=1;
        _rep(j,1,i-1) {
            if (arr[j]<arr[i]) {
                _rep(k,0,p) {
                    f[i][k][0]=(f[i][k][0]+f[j][k][3])%mod;
                    f[i][k][1]=(f[i][k][1]+f[j][k][0]+f[j][k][1])%mod;
                    f[i][k][2]=(f[i][k][2]+f[j][k][2]+f[j][k][4]+f[j][k][5])%mod;
                }
            } else if (arr[j]>arr[i]) {
                _rep(k,0,p) {
                    if (k<arr[j]) {
                        f[i][arr[j]][3]=(f[i][arr[j]][3]+f[j][k][1]+f[j][k][2])%mod;
                    }
                    f[i][k][4]=(f[i][k][4]+f[j][k][3]+f[j][k][4])%mod;
                }
            } else {
                _rep(k,0,p) {
                    f[i][k][5]=(f[i][k][5]+f[j][k][3]+f[j][k][4])%mod;
                }
            }
        }
    }
    int ans=0;
    _rep(i,1,n) {
        _rep(j,0,p) {
            ans=(ans+f[i][j][3]+f[i][j][4])%mod;
        }
    }
    printf("%lld",ans);
    return 0;
}

【AC情况】