问题:
输入N个0~9的整数,可以重复,从小到大打印出这N个数字组成的所有N位数。
e.g
输入:
4002
输出:
0024
0042
0204
0240
0402
0420
2004
2040
2400
4002
4020
4200
策略:
这道题是一个同学问我的,她帮一个同学完成作业。我刚看到问题的时候,第一个想法就是求出全排列,时间复杂度是O(n!)。写个算法除去重复的数列,再写一个算法排序,一个排序算法比如快速排序的平均时间复杂度O(n*lg n)。但也立马否定了。这个算法在整数个数增加后空间复杂度、时间复杂度都会有巨大的增长。这个算法好理解,但也不够巧妙。
其实可以考虑可以在寻找全排列的时候就可以以升序的顺序输出。因为升序数列数字的排列是有规律的。看下面的升序数列:
2345(1)
2354 (2)5提前到第3位
2435 (3)在(1)数列基础上4提前到第2位
2453 (4)5提前了一个位置,似乎是(1)~(2)过程的重复
2534 (5)在(1)数列的基础上将5提前到第2位
2543 (6)4提前了一个位置,似乎是(1)~(2)过程的重复,(5)~(6)似乎是(3)~(4)过程的重复
3245 (7)在(1)数列基础上将3提前到第1位
3254 (8)5提前了一个位置,似乎是(1)~(2)过程的重复
3425 (9)在(7)数列的基础上将4提前到第2位
3452 (10)将5提前到第3位,似乎是(1)~(2)过程的重复,(9)~(10)似乎是(3)~(4)过程的重复
3524 (11)在(7)数列基础上将5提前到第2位
3542 (12)将4提前到第3位,似乎是(1)~(2)过程的重复,(11)~(12)似乎是(3)~(4)过程的重复
4235 (13)在(1)数列的基础上将4提前到第一位
4253 (14)5提前了一个位置,似乎是(1)~(2)过程的重复
4325 (15)在(13)数列基础上将3提前到第2位
4352 (16)将5提前到第3位,似乎是(1)~(2)过程的重复,(15)~(16)似乎是(3)~(4)过程的重复
4523 (17)在(13)数列基础上将5提前到第2位
4532 (18)将3提前到第3位,似乎是(1)~(2)过程的重复,(17)~(18)似乎是(3)~(4)过程的重复,(13)~(18)似乎是(7)~(11)过程的重复
5234 (19)在(1)数列的基础上将5提前到第一位
5243 (20)4提前了一个位置,似乎是(1)~(2)过程的重复
5324 (21)在(19)数列基础上将3提前到第2位
5342 (22)将4提前到第3位,似乎是(1)~(2)过程的重复,(21)~(22)似乎是(3)~(4)过程的重复
5423 (23)在(19)数列基础上将4提前到第2位
5432 (24)将3提前到第3位,似乎是(1)~(2)过程的重复,(23)~(24)似乎是(3)~(4)过程的重复,(19)~(24)似乎是(7)~(11)过程的重复
各位睿智的看官,看出来否?存在一个策略分解这个问题成小问题,而对于每个分解问题存在一个通用的策略击破!对了,睿智如您,这就是分而治之的策略!将它问题分解成更小的问题,再分解成更小的问题。
(1)(2)是子数列4 5的全排列。
(1)~(6)是子数列3 4 5的全排列。(1)(2),(3)(4),(5)(6)分别是子数列3 5,3 4,4 5的全排列。
(1)~(24)是数列2 3 4 5的全排列。(1)~(6),(7)~(12),(13)~(18),(19)~(24)分别是3 4 5,2 4 5,2 3 5,2 3 4的全排列。下面就不列举了额。。。
思考即可发现,对每个输入的子数列,一个通用策略是:
1.从输入数列的倒数第二位作为当前位置开始到子数列开始处结束,迭代执行第2步。
2.在当前位置之后选择一个合适的数字提前到当前位置。(选择数字的策略下面有描述)
3.将当前位置之后的子数列作为输入,转入第1步,寻求子数列的全排列。
这是一个间接的递归调用,程序开始需要先将原始顺序混乱的数列进行升序排序,之后作为输入,调用第1步。可以发现,整个算法中子数列(注意此处指提前操作之后当前位置之后的数列)在调用第1步时始终保持升序有序,以保证最后的输出保持从小到大升序排列)。
注意是提前,不是交换,即不改变当前位置之后的升序顺序。
认真看下这个过程,便可以发现一个选择到提前到当前位置数字的策略。选择之前数列在当前位置之后总是升序排列的。为了使打印出的数列保持升序,选择提前数字时应当从小到大选择。然后将交换之后的目前位置之后的子数列递归调用,进行对它的全排列。还应该考虑数列中出现重复数字的情况。在选择数字时,应当保证提前到当前位置的数字和当前位置并且和前一个选择的数字不同。这样可以避免重复数列的出现。
每次提前数字应当在备份上进行处理,否则会造成混乱,违反了始终保持子数列升序有序的原则。其实当N增大到很大时,其全排列的数目是惊人的,运行会有种刷屏的感觉,:-)。其空间复杂度和时间复杂度是很高的。
实现(C语言):
#include<stdio.h> #include<assert.h> #define MAX_NUM 10 //最大长度,可更改 int numbers[MAX_NUM]; int length; void range(int number[],int st){//排序算法 int i,j; for(i=st;i<length;++i) for(j=st;j<length-1-i;++j) if(number[j]>number[j+1]){ int temp=number[j]; number[j]=number[j+1]; number[j+1]=temp; } } void p_full_arrangement(int[],int); void next_arrange(int in[],int pos){ //通过交换找到下一组局部有序的数列,对应于解题通用策略的第2,3步 int i,cop[MAX_NUM]; for(i=pos+1;i<length;++i){ if(in[i]>in[pos]&&in[i]!=in[i-1]){ //防止出现重复数列的情况,避免与当前位置或者与前一个选择数字相同的数字交换 int j,t; for(t=0;t<length;++t) cop[t]=in[t]; //拷贝数列,在拷贝数列上进行处理 for(j=i;j>pos;j--){ //提前操作 int temp=cop[j]; cop[j]=cop[j-1]; cop[j-1]=temp; } p_full_arrangement(cop,pos+1); //将当前位置之后的子数列得出全排序 } } } void p_full_arrangement(int in[],int pos){//将输入的子数列得到全排列并且打印,对应于解题通用策略中的第1步 int i; for(i=0;i<length;++i) printf("%d",in[i]); printf("/n"); for(i=length-2;i>pos-1;i--){ next_arrange(in,i); } } void full_arrangement(){//先将数列排序再调用全排列的算法 range(numbers,0); p_full_arrangement(numbers,0); } int main(){ int i; printf("Input the length:/n"); scanf("%d",&length); assert(length<=MAX_NUM);//通过断言防止输入的数列长度超出输出的范围 printf("Input the numbers:/n"); for(i=0;i<length;++i) scanf("%d",&numbers[i]); printf("The result:/n"); full_arrangement(); return 0; }
测试结果:
输入为4002时:

输入为23372时:
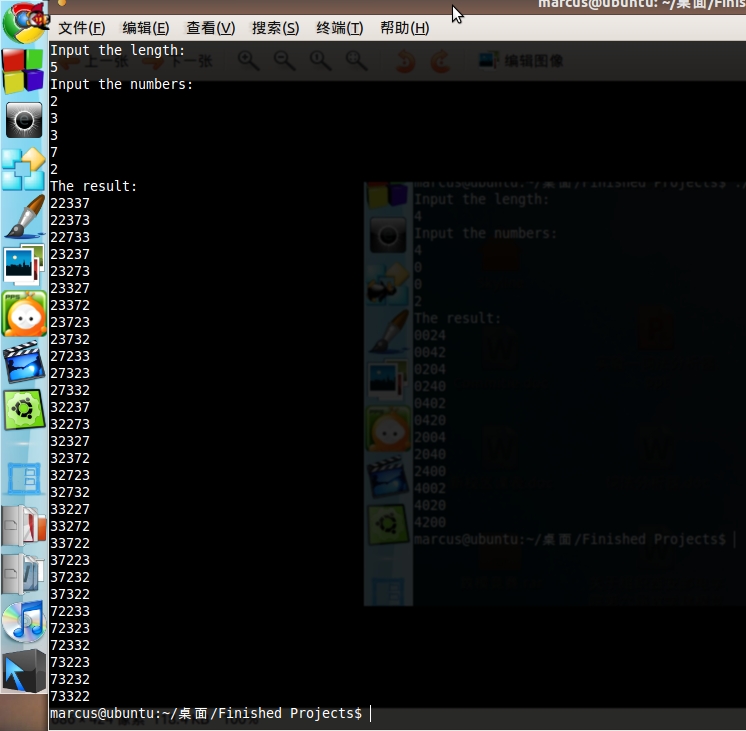
输入为1736542时(部分输出):
算法分析:
算法中长度为n的子数列中next_arrangement的调用次数的递推公式A(n)=n*[A(n-1)+A(n-2)+...+A(2)]+1。A(2)=1(n>2)。total(n)=A(n)+A(n-1)+...+A(2)。total(n)也即为空间复杂度。这个是小于n!的。结果还在研究。。。
算法中主要的工作是复制数组和提前数字,平均提前的幅度是n/2(姑且这么搞哇。。。)。那么时间复杂度就是(3/2)*n*total(n)。



















 1049
1049











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








