《正则表达式识别》

最新推荐文章于 2024-10-20 09:34:58 发布

slavik

最新推荐文章于 2024-10-20 09:34:58 发布

阅读量6.2k

点赞数

文章标签：正则表达式算法 unix null c

本文链接：https://blog.csdn.net/slavik/article/details/1240386

版权

《正则表达式识别》

正则表达式语法

<re>    ::= <expr> { <expr> }
             |   <re> '|' <re>
<expr> ::= <term>
             | <term> '*'
<term> ::= <label>
             | '(' <re> ')'
<label> ::= <symbol>
           | '[' <range> { <range> } ']'
       | '[' '^' <range> { <range> } ']'
<range>::= <symbol>
             | <symbol> '-' <symbol>

<symbol> ::= '.'
                | 0 .. n (any element of alphabet)
                | '/' <symbol>

识别

方法：构造DFA识别正则表达式。

过程：正则表达式 >> 语法树 >> ( NFA >> ) DFA
转化成NFA的过程最好消除掉。

构造语法树

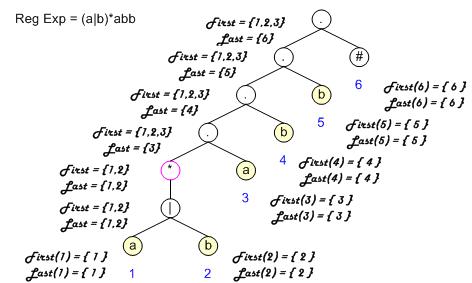
从左向右扫描表达式，自底向上构造二叉树。对每个叶子进行编号。
＃号表示结束，实际并不存在。

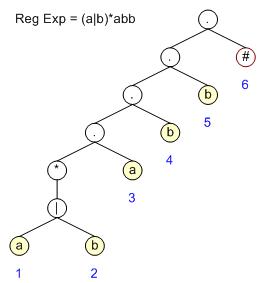
构造NFA

先构造NFA，进行观察。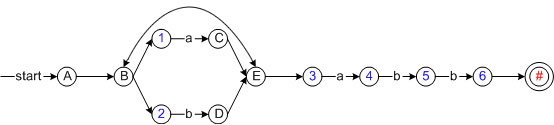

比较语法树和NFA

语法树中的叶子，和NFA中的所有非空输入结点一一对应。其他都是空输入。

从NFA构造DFA（不含空输入）

从NFA构造DFA，本质上是对任意可接收输入后所有可能的NFA的状态的穷举。
所以DFA的起始状态是空输入后的NFA状态集合。
S = e-closure(A)
DFA的一个状态X接受输入a后的状态X'是
X' = U e-closure(s) s 属于X含有的NFA状态接受输入a后到达的NFA状态集合。

这样得到DFA

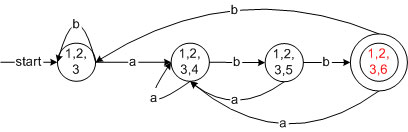
比较DFA和NFA

对于只有空输入的NFA结点，他们没有必要出现在DFA中。
首先，相邻的只含有空输入的结点，可以合并成一个结点。他们的e-closure完全相同。所以他们在DFA里的价值一样。因为同样输入可以达到相同的e-closure。
其次，他们在DFA的状态中对可接受的输入没有影响。只有非空的NFA结点，可以选择输入。一个DFA状态，只受它包含的NFA非空输入状态的影响。

比较DFA和语法树

只有语法树的叶子对于DFA有意义。
叶子代表了接受一个特定非空输入的状态。

叶子肯定是非空的，必须有输入才能通过这个状态，到其他状态。
一个子树的根，根据构造顺序，是遍历完子树后才通过的状态。如果这个状态可以为空，则说明可以不输入这个子树含有的表达式。

对于二叉树，如果左孩子可以为空，则说明可以先通过右孩子；如果右孩子可以为空，则说明通过左孩子后，可以不经过右孩子；如果左右都可以为空，说明可以不经过任何孩子。
根据前面得到的，对DFA有意义的只有叶子结点的结论。一棵子树能够产生的状态，就是所有可能的遍历情况下包含的叶子集合。

对于任意子树，存在一个能够进入它的状态集合，和离开它时候的状态集合。

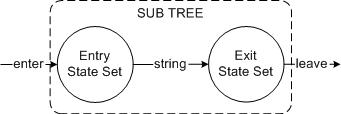
对于叶子结点，它能产生的状态只有自己。必须先从自己进入，再从自己出去。
对于连接运算，如果它的左孩子不能为空，那么它只能先通过左孩子的进入状态集合；如果左孩子可以为空，那么可以从左孩子和右孩子的进入集合的并集进入；如果它的右孩子不可为空，则只能从右孩子的离开状态出去；如果它的右孩子可以为空，则可以从右孩子和左孩子的离开集合并集离开。
对于或运算，它总是先进入左右孩子的进入集合并集，再从左右孩子的离开集合并集离开。
对于星号运算（它只有一个左孩子），它从左孩子的进入集合进入，从左孩子的离开集合离开。

再考虑可为空的特性。

叶子结点，不能为空，因为必须有输入才能通过。
连接运算只要有一个孩子不为空，就不能为空。当且仅当两个孩子都可为空时为空。
或运算只要有一个孩子能为空，就可以为空。当且仅当两个孩子都不为空是，不能为空。
星号运算一定可以为空。（加号运算其实是不能为空的星号运算）

将进入状态命名为first，离开命名为last，可为空命名为Nullable。

计算First Last Nullable

根据前面的内容得到以下表达式。

对示例语法树求First Last 集合和Nullable属性。红色圈表示可以为空，其他的不可为空。

跟随集合

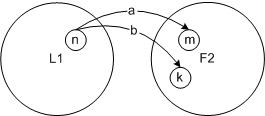
对于连接运算

F2中的所有状态都可能跟随在L1的状态后面。换句话，L1里的状态，有转移到F2中的情况。

对于星号运算

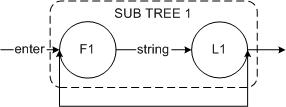
F1中的所有状态都可能跟随在L1的状态后面。

或运算不不需要考虑。因为两个孩子不分先后出现。而且互相排斥。不会出现他们代表的字符串连接的情况。

这里把一个状态可能的跟随状态集合定义为Follow。

重新观察DFA，一个DFA的状态的一个转移，是这个DFA状态中含有的NFA叶子对于一个输入，可能到达的NFA叶子的集合。
所以只要知道起始DFA状态，和NFA叶子的Follow，变可以遍历出DFA。

根据前面的连接和星号运算的规则，可以在构造树的同时得到每个叶子的Follow集合。

Follow(1) = { 1, 2, 3 }
Follow(2) = { 1, 2, 3 }
Follow(3) = { 4 }
Follow(4) = { 5 }
Follow(5) = { 6 }
Follow(6) = NULL 终止结点

从新观察DFA

状态（1，2，3）接受a到状态（1，2，3，4）。
可以接受a的有叶子1，3。
Follow(1) U Follow (3) = { 1, 2, 3, 4 }

对于DFA状态N，它含有的所有能够接受输入a的叶子的Follow集合并集，含有了所有可能的NFA转移。这和把NFA转换成DFA的过程一致。
所以，在构造玩语法树的同时，已经完成了得到DFA，所需要的数据。

从语法树直接构造DFA

根据First集合的定义

起始状态为语法树根的First集合。

S = First(root)
N ＝ S
开始循环遍历

标记N为已经遍历。
对于N含有的每个叶子i，集合<N, char_of(i)> = < N, char_of(i) > U follow(i)
对于每一个<N, a >，如果还没有相同的状态出现（含有同样的叶子），添加未标记状态State(<N,a>)。如果状态含有叶子＃，则为结束状态。
对于每一个<N, a >，添加转移函数 Tran(N, a) = State(<N, a>)。
N ＝任意一个未标记状态

如果没有未标记结点，退出循环。

这样得到识别正则表达式的

范围输入

范围输入描述了一个可以接受的范围，比如0－9，a－z，A－Z之类的。
a－z可以等价为a|b|c|...|z。

但是这样会增加很多叶子，以及同样多的运算符结点。在转换DFA的过程中会增加很多运算。
因为转换算法只和叶子个数有直接关系。运算符已经在构造语法树时处理了。

重新研究语法树的集合计算过程。如果把范围拆分成或运算，这样会出现一组永远同时出现的叶子在或运算的First和Last集合。
由于他们永远同时出现，所以他们的follow集合也一样。这样可以把他们转换成一个可以接受多个输入的叶子。

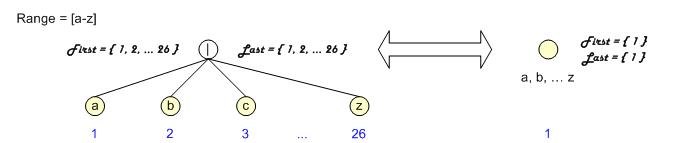
既便范围大到包括所有的可能输入，比如ASCII全表，也只要一个叶子就可以表示了。

为了处理可以接受多个输入的叶子，需要修改DFA转化算法。

S = First(root)
N ＝ S
开始循环遍历

标记N为已经遍历。
对于N含有的每个叶子i，对于叶子i的每一个输入a，集合<N, a> = < N, a > U follow(i)
对于每一个<N, a >，如果还没有相同的状态出现（含有同样的叶子），添加未标记状态State(<N,a>)。如果状态含有叶子＃，则为结束状态。
对于每一个<N, a >，添加转移函数 Tran(N, a) = State(<N, a>)。
N ＝任意一个未标记状态

如果没有未标记结点，退出循环。

通配符

通配符本质和范围输入一样，所以可以采用范围输入的实现。
对于UNIX风格的正则表达式，通配符只有一个点号，它代表非换行/n的任何输入。等价为范围0x1～0x9， 0xB（11）～0x7E（126）。

起始运算

运算符^可以强制正则表达式必须从字符串起始位置开始匹配。
实际上之前生成的DFA也只能从起始位置开始匹配。

那么怎么才能让它从任意位置开始匹配呢。
一个简单而且高效率的方法是在开头加入“ .*”，这样就可以在头部匹配任意字符，直到实际的正则表达式开始。
而且这个方法效率远远高于反复尝试新的开始位置，因为这个方法可以利用之前的比较结果，减少比较次数。原理可以参考KMP字符串比较算法。