对于普通的网络流来说, dinic或者ISAP的O(n²m
)复杂度可能就够了, 但考虑如下问题:

如图所示的一个平面, 源点为左上角, 汇点为右下角, 边数范围到了1000, 这时候O(n²m)的复杂度显然不合适了。 当然, 现在我学会了独特的处理技巧, 专业处理此类平面图问题。
---------------------------------------------------------------------------------------------------------------------------------------------
我们需要一种特殊的建图方式。 首先我们将整个平面图划分的区域新建成点, 考虑这样的一条边e(a, b), 表示连接a、b且权值为w的边, 这条边将平面分为两部分A、B,那么在新的图中建立一条无向边E(A, B), 边权同样为w(如图1)。 按照这种方法建图, 我们得到了一个新的图。

图1
在得到一个新图后, 在不破坏新图的前提下从源点到汇点连一条虚边, 这条虚边又构造出一个新的平面, 记这个平面为s, 无限大的平面为t, 那么s到t的一条路径即为原图的一个割。 这一点很好证明, 就像一刀切了下去, 原图变成了二分图(如图2)。
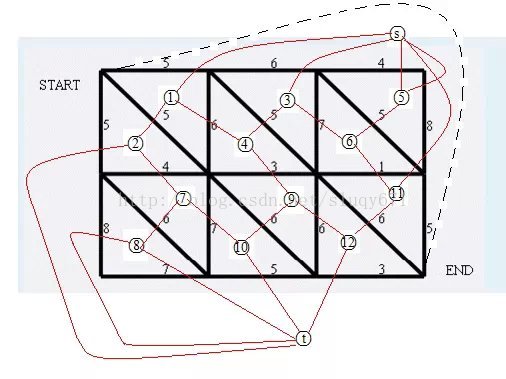
图2
这样一来, 求网络流的方法也很方便了, 由最大流-最小割定理可知, 答案就是s到t的最短路径, 这对应的是一个最小割。

如图所示的一个平面, 源点为左上角, 汇点为右下角, 边数范围到了1000, 这时候O(n²m)的复杂度显然不合适了。 当然, 现在我学会了独特的处理技巧, 专业处理此类平面图问题。
---------------------------------------------------------------------------------------------------------------------------------------------
我们需要一种特殊的建图方式。 首先我们将整个平面图划分的区域新建成点, 考虑这样的一条边e(a, b), 表示连接a、b且权值为w的边, 这条边将平面分为两部分A、B,那么在新的图中建立一条无向边E(A, B), 边权同样为w(如图1)。 按照这种方法建图, 我们得到了一个新的图。

图1
在得到一个新图后, 在不破坏新图的前提下从源点到汇点连一条虚边, 这条虚边又构造出一个新的平面, 记这个平面为s, 无限大的平面为t, 那么s到t的一条路径即为原图的一个割。 这一点很好证明, 就像一刀切了下去, 原图变成了二分图(如图2)。

图2
这样一来, 求网络流的方法也很方便了, 由最大流-最小割定理可知, 答案就是s到t的最短路径, 这对应的是一个最小割。
---------------------------------------------------------------------------------------------------------------------------------------------
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <cstdlib>
#define N 2000000 + 100
#define M 6000000 + 100
#define INF 1000000000
using namespace std;
struct edge
{
int to, w, next;
}e[M];
struct node
{
int now, dist;
node() { }
node(int x, int y)
{
now = x;
dist = y;
}
bool operator < (const node x) const
{
return dist > x.dist;
}
};
int n, m, num, sum, p[N], d[N], flag[N];
void read(int &x)
{
x = 0;
char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9')
{
x = 10*x + c - '0';
c = getchar();
}
}
void add(int x, int y, int z)
{
e[++num].to = y;
e[num].w = z;
e[num].next = p[x];
p[x] = num;
}
void init()
{
int x, y, z, l, r, po;
read(n), read(m);
if (n == 1 || m == 1)
{
if (n > m) swap(n, m);
int ans = INF;
for (int i = 1; i < m; ++i)
{
read(x);
if (x < ans) ans = x;
}
printf("%d\n", ans);
exit(0);
}
l = n - 1, r = m - 1;
sum = 2 * l * r;
for (int i = 1; i <= n; ++i)
for (int j = 1; j < m; ++j)
{
read(z);
po = (i-1)*r + j;
y = po << 1;
x = y - 2*r - 1;
if (i == 1) x = 0;
else if (i == n) y = sum + 1;
add(x, y, z);
add(y, x, z);
}
for (int i = 1; i < n; ++i)
for (int j = 1; j <= m; ++j)
{
read(z);
po = (i-1)*r + j - 1;
x = po << 1;
y = x | 1;
if (j == 1) x = sum + 1;
else if (j == m) y = 0;
add(x, y, z);
add(y, x, z);
}
for (int i = 1; i < n; ++i)
for (int j = 1; j < m; ++j)
{
read(z);
po = (i-1)*r + j;
y = po << 1;
x = y - 1;
add(x, y, z);
add(y, x, z);
}
}
void dij_heap()
{
priority_queue<node>q;
for (int i = 1; i <= sum; ++i)
d[i] = INF;
d[sum+1] = INF;
q.push(node(0, 0));
while(!q.empty())
{
int x = q.top().now;
q.pop();
if (flag[x]) continue;
for (int i = p[x]; i; i = e[i].next)
{
int k = e[i].to;
if (d[k] > d[x] + e[i].w)
{
d[k] = d[x] + e[i].w;
q.push(node(k, d[k]));
}
}
}
}
void deal()
{
dij_heap();
printf("%d\n", d[sum+1]);
}
int main()
{
init();
deal();
return 0;
}





















 2218
2218

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








