用walshall算法求解离散数学中的传递闭包问题

用warshall算法求传递闭包

从“插入”的视角理解该算法

首先我在网上查阅资料并且结合自己的理解以及数学层面的推理论证，在代码层面给出了用warshall算法求传递闭包的算法。其核心代码如下：

 void Warshall(int nearArra[100][100],int row,int column) {
     //Warshall算法求运用邻接矩阵求图中所有可能的通路（即可达矩阵）
     //参数 ： 图的邻接矩阵，矩阵的行数，列数
     for (int k = 0; k < column; k++) {
         for(int i=0;i<row;i++)
             for (int j = 0; j < column; j++) {
                 if ([i][j] == 1)
                     ;//如果“捷径”已经存在，则不需要再用新的结点k作为媒介
                 else if (nearArra[i][k] == 1 && nearArra[k][j] == 1)//i结点和j结点之间存在长度为2的结晶
                 {
                     nearArra[i][j] = 1;
                 }
                 else
                     ;
         }
     }
 }

如上所示，在warshall算法中，每一次循环都是基于某个k值进行的处理，这个k对应着原来图的n个结点中的一个，每一层循环内部都会把k视为“媒介点”，遍历当前邻接矩阵的所有元素，如果nearArra【i】【j】 == 1，说明从i结点到j结点之间已经存在长度为1的可达路径，所以不做任何处理，而如果nearArra【i】【j】 ==0，那么就通过判断nearArrai == 1 && nearArrak == 1的真假来判断k是否可以作媒介结点，如果可以，那就把nearArra【i】【j】置为1。就这样，让k从0遍历到n，每个结点都作为媒介结点进行遍历之后所得到的矩阵就会蕴含原来的图中所有可能的可达关系，也就是表示了原来关系的传递闭包关系。

结果验证：

经过验证，结果符合预期。

深入探讨

刚才只是在代码层面证明了算法的正确性，但是理论层面的证明尚有不足。

下面就我在研究这段代码时思考了如下问题：

传递闭包要求的是要把原来的关系中的所有可能的“捷径”都包括进去，这些捷径在原来的关系中的“长度”显然不一定是2，但是在上述的代码中，显然只是考虑了长度为2的路径，这样不会造成情况的遗漏吗？

只考虑长度为2的路径，乍一看确实不对，但是实际上并非如此，因为对于原来的邻接矩阵来说，如果长度为n的路径之间存在长度为1的捷径，那么这个捷径必然也可以看成是长度为2的路径的捷径，如下图所示：

换句话说，

如果长度为k（k为2到n之间的任意数）的路径存在捷径，那么这条捷径一定也可以看作是由长度为2的路径简化而来。

下面，如果能证明本程序能够遍历所有长度为2的路径，那么就可以证明最终得到的nearArra矩阵将包括所有的“捷径”，即是原来关系的传递闭包。

我一开始觉得上面的程序不能遍历所有的长度为2的可能路径，原因结合如下图说明

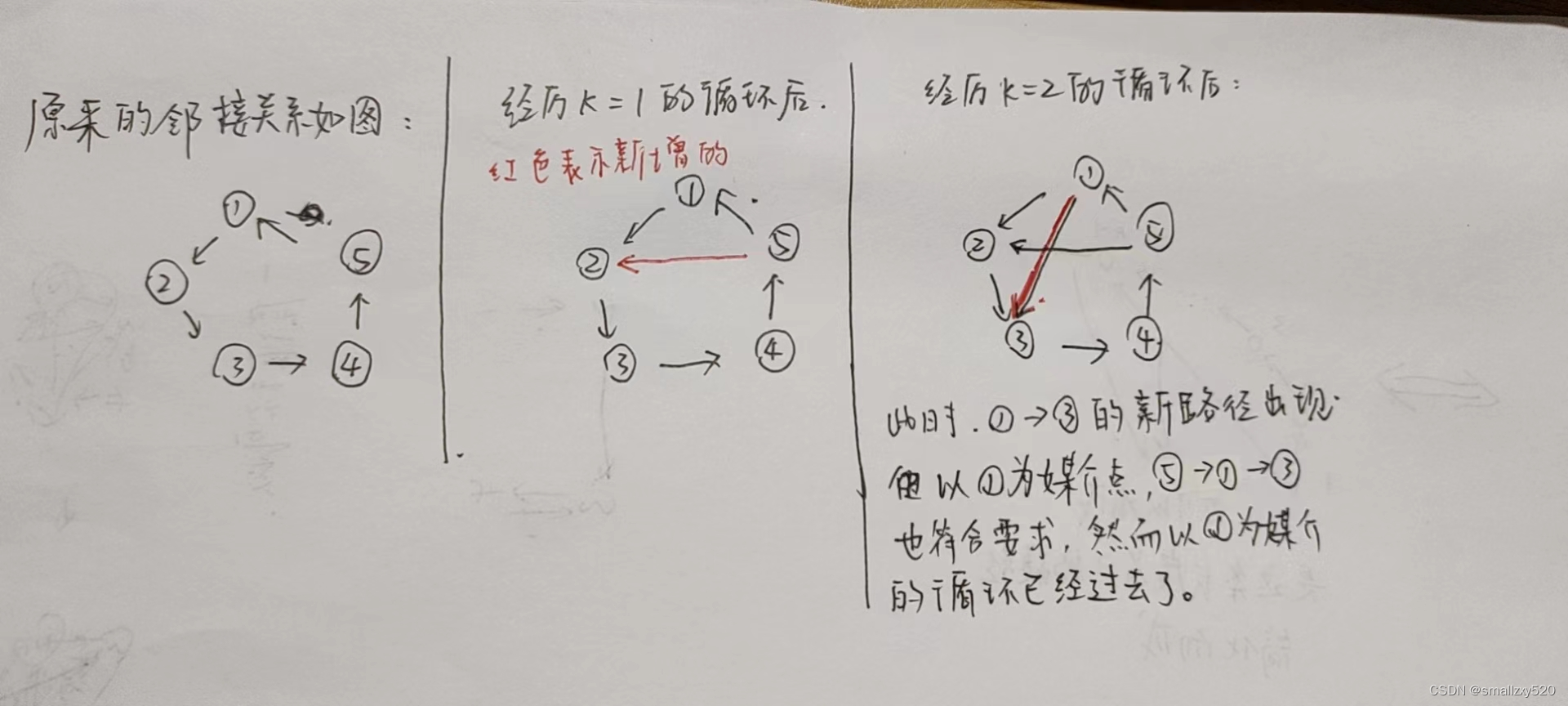
如上图所示，后续可能会让1结点出现指向新的结点的路径，比如上述案例中的1->3,这就意味着以1结点为媒介还会有之前未出现过的情况，在上述案例中就是5->1->3这条，这么乍一看，似乎会漏掉一些“捷径”，但是实际上并不会，因为从结果上来看，5->1->3的最终结果就是形成5结点和3结点之间的捷径，而5->3这条新的捷径一定要以1为媒介实现吗？显然不是！它也可以以2结点为媒介来实现，而2结点正是当前正作为媒介点的k，所以说，从结果上来看，并不会有“捷径”的缺失。

 

综上所述，原来的程序可以实现求原来关系的传递闭包关系的功能。

对warshall算法的一个更简明扼要的理解方式

还是上面那段程序：

 void Warshall(int nearArra[100][100],int row,int column) {
     //Warshall算法求运用邻接矩阵求图中所有可能的通路（即可达矩阵）
     //参数 ： 图的邻接矩阵，矩阵的行数，列数
     for (int k = 0; k < column; k++) {
         for(int i=0;i<row;i++)
             for (int j = 0; j < column; j++) {
                 if ([i][j] == 1)
                     ;//如果“捷径”已经存在，则不需要再用新的结点k作为媒介
                 else if (nearArra[i][k] == 1 && nearArra[k][j] == 1)//i结点和j结点之间存在长度为2的结晶
                 {
                     nearArra[i][j] = 1;
                 }
                 else
                     ;
         }
     }
 }

对nearArra给出如下定义：在经历第k层的循环之后的nearArra，nearArra【i】【j】==1当且仅当在R的关系图中存在一条从结点i到结点j的路径，并且这条路径除去端点外，中间只经过{0，1，2，……k}中间的结点。nearArra的初始状态（k=0之前）就是原来的邻接关系矩阵，而当k=n时就表示我们所要求的传递闭包关系。

所以，问题的关键就在于从k到k+1的迭代：对于第k+1层循环中的任意nearArra【i】【j】来说，如果已经等于1，说明只经过{0，1，2，……k}中间的结点就可以实现从i结点到j结点，由于{0，1，2，……k}是{0，1，2，……k，k+1}的子集，所以对于第k+1层的nearArra来说，nearArra【i】【j】仍为1；而如果当前的nearArra【i】【j】=0，说明只经过{0，1，2，……k}中的结点不能实现从i到j，这时再考虑能否以k+1为媒介结点实现从i到j，如果满足nearArra【i】【k+1】== 1 &&nearArra【k+1】【j】 == 1，那也把第k+1层的nearArra的nearArra【i】【j】设置为1。（以nearArra【i】【k+1】== 1为例，它的意义是在前一层循环之后的nearArra存在从i结点到k+1结点的路径，后者同理。）

所以，这样一层一层迭代下去。最终的nearArra对应原关系的传递闭包。

反思

不难感觉到我的第一种理解方式十分繁琐，但是下面从另一个视角来看待该程序，就会发现同样的一段程序，你看待它的角度不同，理解的繁琐程度和复杂程度会有很大差异！这也给了我一点教训：在用某一种方式理解一段程序或者算法十分繁琐、麻烦的时候，可以尝试转换一下看待这段程序的角度。