二叉树的非递归遍历

最新推荐文章于 2020-10-13 17:02:21 发布
最新推荐文章于 2020-10-13 17:02:21 发布
阅读量2.7k 收藏 2
点赞数 1
分类专栏： 数据结构 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/snow_5288/article/details/53870166
版权

测试环境：VS 2010

上篇文章我们实现了二叉树：http://blog.csdn.net/snow_5288/article/details/53672367


        现在，简单说下二叉树的非递归遍历（其他函数也可按照相似的方式用非递归实现）。以前我们知道，凡是可用递归实现的代码我们都可用栈来模拟它，今天就来简单模拟实现一下二叉树的非递归遍历，上述链接中的其他函数也可通过栈来进行模拟，因为遍历应用比较广泛，所以我只对它进行改写，其他函数有兴趣的可自己仿照实现，如若有问题随时欢迎来打扰我吐舌头偷笑大笑


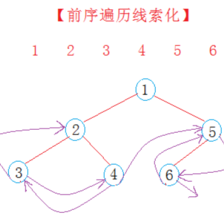
1、先序遍历

基本思想：

1>首先定义一个栈，每遇到一个节点，就对其数据进行访问；然后将其入栈，将当前节点的左孩子赋给它，循环此过程，直到最左节点被访问并被压入栈中。

2>出循环后用临时变量保存栈顶节点，然后对栈顶节点进行出栈操作，到此说明当前节点以及其左子树已被访问过了。

3>将临时变量的右孩子赋给当前节点，用子问题的方式去访问其右子树。

void preorderR(Node* root)//先序遍历打印树的各个节点
	{
		Node* cur = root;
		stack<Node*> s;
		while (!s.empty() || cur)//只要当前节点和栈不同时为空，就说明树没遍历完
		{
			while(cur)//先序遍历，遇到树根节点直接访问数据并将其压栈
			{
				cout<<cur->_value<<" ";
				s.push(cur);
				cur = cur->_lchild;
			}

			Node* top = s.top();//取出栈顶元素，到此说明此节点以及其左子树已经访问过了
			s.pop();

			cur = top->_rchild;//以子问题的方式去访问右子树
		}
		cout<<endl;
	}


2、中序遍历

基本思想：

1>首先定义一个栈，每遇到一个节点，就将其入栈，将当前节点的左孩子赋给它，循环此过程，直到最左节点将其压入栈中。

2>出循环后用临时变量保存栈顶节点，访问栈顶节点的数据，然后对栈顶节点进行出栈操作，到此说明当前节点的左子树以及当前节点已被访问过了。

3>将临时变量的右孩子赋给当前节点，用子问题的方式去访问其右子树。

	void inorderR(Node* root)//中序遍历打印树的各个节点
	{
		Node* cur = root;
		stack<Node*> s;
		while(!s.empty() || cur)//只要当前节点和栈不同时为空，就说明树没遍历完
		{
			while(cur)//中序遍历，遇到树根节点直接将其压栈
			{
				s.push(cur);
				cur = cur->_lchild;
			}

			Node* top = s.top();//取出栈顶元素，到此说明此节点的左子树已经访问过了
			cout<<top->_value<<" ";//访问栈顶元素（即根节点）
			s.pop();

			cur = top->_rchild;//以子问题的方式去访问右子树
		}
		cout<<endl;
	}


3、后序遍历

1>首先定义一个栈和一个记录上一个被访问节点的变量，每遇到一个节点，就对其数据进行访问；然后将其入栈，将当前节点的左孩子赋给它，循环此过程，直到最左节点被访问并被压入栈中。

2>出循环后用临时变量保存栈顶元素，只有当前节点的右子树为空或者其右子树已经访问过时，才能对当前节点进行访问，同时将栈顶元素出栈

3>将临时变量的右孩子赋给当前节点，用子问题的方式去访问其右子树。


void postorderR(Node* root)//后序遍历打印树的各个节点
	{
		Node* cur = root;
		Node* prev = NULL;//上一个访问过的数据
		stack<Node*> s;
		while(!s.empty() || cur)//只要当前节点和栈不同时为空，就说明树没遍历完
		{
			//后序遍历，遇到树根节点直接将其压栈
			while(cur)
			{
				s.push(cur);
				cur = cur->_lchild;
			}

			Node* top = s.top();//取栈顶元素，但不一定能访问
			
			//当节点右子树为空或已经访问过时对其直接进行访问
			if (top->_rchild==NULL || top->_rchild==prev)
			{
				cout<<top->_value<<" ";
				prev = top;//将prev更新为已经访问的节点
				s.pop();
			}
			else//以子问题的方式去访问右子树
			{
				cur = top->_rchild;
			}
	   }
		cout<<endl;
	}

完整的代码及测试：

#include <iostream>
#include <cassert>
#include <queue>
#include <stack>
using namespace std;

template <class T>
struct TreeNode
{
	TreeNode(const T& value = T())
		:_value(value)
		,_lchild(0)
		,_rchild(0)
	{}
	T _value;//节点的值
	TreeNode<T>* _lchild;//左孩子
	TreeNode<T>* _rchild;//右孩子
};

template <class T>
class BinaryTree
{
public:
	typedef TreeNode<T> Node;
	BinaryTree()//无参构造函数
		:_root(NULL)
	{}
	BinaryTree(const T* a,size_t size,const T& invalid)//构造函数
	{
		assert(a);
		size_t index = 0;
		_root = CreatTree(a,size,invalid,index);
	}
	BinaryTree(const BinaryTree<T>& b)//拷贝构造
	{
		_root = Copy(b._root);
	}
	//现代写法的赋值运算符重载1
	BinaryTree& operator=(const BinaryTree<T>& b)
	{
		if (this != &b)
		{
			Node* tmp = Copy(b._root);
			Destroy(_root) ;
			_root = tmp;
			//swap(_root,tmp);
		}
		return *this;
	}
	现代写法的赋值运算符重载2
	//BinaryTree& operator=(BinaryTree<T> b)
	//{
	//	swap(b._root,_root);
	//	return *this;
	//}
	~BinaryTree()//析构
	{
		if (NULL != _root)
		{
			Destroy(_root);
			_root = NULL;
		}
	}
	void PreOrder()//先序遍历打印树的各个节点
	{
		cout<<"先序遍历:";
		preorderR(_root);
		cout<<endl;
	}
	void InOrder()//中序遍历打印树的各个节点
	{
		cout<<"中序遍历:";
		inorderR(_root);
		cout<<endl;
	}
	void PostOrder()//后序遍历打印树的各个节点
	{
		cout<<"后序遍历:";
		postorderR(_root);
		cout<<endl;
	}
	void LevelOrder()//层序遍历打印树的各个节点
	{
		cout<<"层序遍历:";
		levelorder(_root);
		cout<<endl;
	}
	size_t Size()//求树中的节点个数
	{
		cout<<"size:";
		return size(_root);
	}
	size_t Depth()//求树的深度
	{
		cout<<"depth:";
		return depth(_root);
	}
	size_t GetLeafSize()
	{
		cout<<"leaf_size:";
		return getleafsize(_root);
	}
	size_t GetKLevelSize(size_t k)//树中第k层的节点个数
	{
		cout<<k<<"_level_size:";
		return getklevelsize(_root,k);
	}
protected:
	//按照先序遍历递归建树
	Node* CreatTree(const T* a,size_t size,const T& invalid,size_t& index)//注意index的传值方式
	{
		assert(a);
		Node* root = NULL;
		if (a[index] != invalid && index < size)//按先序遍历建树
		{
			root = new Node(a[index]);
			root->_lchild = CreatTree(a,size,invalid,++index);
			root->_rchild = CreatTree(a,size,invalid,++index);
		}
		return root;
	}
	//拷贝对象
	Node* Copy(Node* root)
	{
		Node* tmp = NULL;

		if(root)
		{
			tmp = new Node(root->_value);
			tmp->_lchild = Copy(root->_lchild);
			tmp->_rchild = Copy(root->_rchild);
		}
		return tmp;
	}
	//释放空间
	void Destroy(Node*& root)
	{
		if(root)//用后序遍历方式释放空间
		{
			Destroy(root->_rchild);
			Destroy(root->_lchild);
			delete root;
			root = NULL;
		}
	}
	void preorderR(Node* root)//先序遍历打印树的各个节点
	{
		Node* cur = root;
		stack<Node*> s;
		while (!s.empty() || cur)//只要当前节点和栈不同时为空，就说明树没遍历完
		{
			while(cur)//先序遍历，遇到树根节点直接访问数据并将其压栈
			{
				cout<<cur->_value<<" ";
				s.push(cur);
				cur = cur->_lchild;
			}

			Node* top = s.top();//取出栈顶元素，到此说明此节点以及其左子树已经访问过了
			s.pop();

			cur = top->_rchild;//以子问题的方式去访问右子树
		}
		cout<<endl;
	}
	void inorderR(Node* root)//中序遍历打印树的各个节点
	{
		Node* cur = root;
		stack<Node*> s;
		while(!s.empty() || cur)//只要当前节点和栈不同时为空，就说明树没遍历完
		{
			while(cur)//中序遍历，遇到树根节点直接将其压栈
			{
				s.push(cur);
				cur = cur->_lchild;
			}

			Node* top = s.top();//取出栈顶元素，到此说明此节点的左子树已经访问过了
			cout<<top->_value<<" ";//访问栈顶元素（即根节点）
			s.pop();

			cur = top->_rchild;//以子问题的方式去访问右子树
		}
		cout<<endl;
	}
	void postorderR(Node* root)//后序遍历打印树的各个节点
	{
		Node* cur = root;
		Node* prev = NULL;//上一个访问过的数据
		stack<Node*> s;
		while(!s.empty() || cur)//只要当前节点和栈不同时为空，就说明树没遍历完
		{
			//后序遍历，遇到树根节点直接将其压栈
			while(cur)
			{
				s.push(cur);
				cur = cur->_lchild;
			}

			Node* top = s.top();//取栈顶元素，但不一定能访问
			
			//当节点右子树为空或已经访问过时对其直接进行访问
			if (top->_rchild==NULL || top->_rchild==prev)
			{
				cout<<top->_value<<" ";
				prev = top;//将prev更新为已经访问的节点
				s.pop();
			}
			else//以子问题的方式去访问右子树
			{
				cur = top->_rchild;
			}
	   }
		cout<<endl;
	}
	
	void levelorder(Node* root)//层序遍历打印树的各个节点
	{
		queue<Node*> q;
		if (root)
		{
			q.push(root);//将根节点插进队列
		}
		while(!q.empty())
		{
			Node* front = q.front();
			q.pop();
			cout<<front->_value<<" ";
			if (front->_lchild)
			{
				q.push(front->_lchild);
			}
			if (front->_rchild)
			{
				q.push(front->_rchild);
			}
		}
	}
	size_t size(Node* root)//求树中的节点个数
	{
		size_t count = 0;
		if (NULL == root)
		{
			count = 0;
		}
		else
		{
			//当前节点 = 左子树节点 + 右子树节点 + 1
			count = size(root->_lchild) + size(root->_rchild)+ 1;
		}
		return count;
	}
	size_t depth(Node* root)//求树的深度
	{
		if (NULL == root)
		{
			return 0;
		}
		else
		{
			return depth(root->_lchild)>depth(root->_rchild)?
				(depth(root->_lchild)+1):(depth(root->_rchild)+1);
		}
	}
	size_t getleafsize(Node* root)//求叶节点的个数
	{
		if (NULL == root)//空树
		{
			return 0;
		}
		if (NULL == root->_lchild && NULL == root->_rchild)//左叶节点右节点均为空，即
		{
			return 1;
		}
		else//左子树的叶节点+右子树的叶节点
		{
			return getleafsize(root->_lchild)+getleafsize(root->_rchild);
		}
	}
	size_t getklevelsize(Node* root,size_t k)//树中第k层的节点个数
	{
		assert(k>0);

		size_t count = 0;
		if (NULL == root)
		{
			return 0;
		}
		if (k == 1)
		{
			count++;
		}
		else
		{
			count =  getklevelsize(root->_lchild,k-1)
				+ getklevelsize(root->_rchild,k-1);
		}
		return count;
	}
protected:
	Node* _root;//根节点
};

void TestBinaryTree()
{
	int arr[] = {1, 2, 3, '#', '#', 4, '#' , '#', 5, 6,'#','#','#'};
	size_t size = sizeof(arr)/sizeof(arr[0]);
	BinaryTree<int> bt(arr,size,'#');
	BinaryTree<int> b1(bt);
	BinaryTree<int> b2;
	b2 = bt;
	b2.PreOrder();
	b2.InOrder();
	b2.PostOrder();
	b2.LevelOrder();
	cout<<b2.Size()<<endl;
	cout<<b2.Depth()<<endl;
	cout<<b2.GetLeafSize()<<endl;
	cout<<b2.GetKLevelSize(1)<<endl;
	cout<<b2.GetKLevelSize(2)<<endl;
	cout<<b2.GetKLevelSize(3)<<endl;
}

int main()
{
	TestBinaryTree();
	system("pause");
	return 0;
}
测试结果：





snow_5288
关注
专栏目录
二叉树非递归遍历
每天进步一点点
06-14 944
面试的时候可能会问到二叉树的非递归遍历。 下面是自己写一些二叉树遍历的非递归的代码，仅供参考： 二叉树节点： class TreeNode { //二叉树节点 int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } 二叉树前序遍历非递归 代码： public
非递归遍历二叉树
热门推荐
重剑无锋
09-05 5万+
1.先序遍历从递归说起void preOrder(TNode* root){    if (root != NULL)    {        Visit(root);        preOrder(root->left);        preOrder(root->right);    }}递归算法非常的简单。先访问跟节点，然后访问左节点，
数据结构6——二叉树（非递归遍历）
weixin_30684743的博客
03-17 263
之前讲了递归调用二叉树，下面简单的介绍非递归二叉树遍历。 非递归二叉树遍历是采用的栈的方式，将结点分为，根节点，左子树，右子树的顺序分别在不同的时候入栈和出栈。 1：非递归前序遍历（DLR） 1 /* 2 * 非递归二叉树遍历方法 3 */ 4 public class BinTreeNoRecur { 5 6 //非递归的方法实现和...
非递归二叉树遍历
lanxinglan的专栏
12-08 909
非递归二叉树遍历是面试中最容易问道的问题，其可以考察应聘者对二叉树遍历的掌握程度，又可以测试出面试者的编码能力。
C++实现二叉树非递归遍历方法实例总结
09-04
总结来说，C++实现二叉树非递归遍历的关键在于理解遍历的顺序，并巧妙地利用栈来模拟递归过程。这种方法不仅适用于面试，而且在实际编程中也具有较高的效率和灵活性。通过熟练掌握这些技巧，可以更好地理解和解决与...
二叉树非递归遍历.rar
02-20
查找算法，二叉排序树，二叉树层次遍历，二叉树非递归遍历，二叉树的建立，关键字匹配查找等。 如有问题，可随时私信。 初学C语言必须掌握的一些基础知识，包括直接选择排序、直接插入排序、冒泡排序、快速排序。 ...
二叉树非递归遍历-二叉树非递归遍历-二叉树非递归遍历-二叉树非递归遍历
最新发布
09-09
/*********************************************************** ***********************************************************/ #include #include #include #define MS 50 struct BTreeNode ...
遍历二叉树的4个非递归算法.rar_binary tree_二叉树_二叉树 非递归 遍历_递归_遍历 CSharp
09-14
本资源"遍历二叉树的4个非递归算法.rar"提供了C#语言实现的这四种非递归遍历方法，对于学习者来说是非常宝贵的资料。 1. **前序遍历**（Root-Left-Right）： 在前序遍历中，我们首先访问根节点，然后递归地遍历左...
二叉树的非递归实现
helinsen的专栏
06-21 507
http://www.cnblogs.com/dolphin0520/archive/2011/08/25/2153720.html
二叉树的递归遍历和非递归遍历（附详细例子）
毛毛虫的小哈
06-06 9952
二叉树的递归遍历和非递归遍历（附详细例子）         二叉树的遍历主要有递归实现和非递归实现，递归实现比较好理解，非递归实现主要是利用了栈的思想，后进先出，本文实现二叉树的非递归遍历主要是用了LinkedList可以当做栈使用的功能。具体例子如下： package com.sheepmu; import java.util.LinkedList; public class Bin
二叉树非递归
zhj_fly的博客
08-12 351
1、先序非递归 先序遍历：根->左->右 先序非递归最简单，使用栈保存节点。节点出栈后，直接访问（输出值或者保存下来），然后将右孩子加入栈，再将左孩子加入栈（注意左右的顺序）。 #include <iostream> #include <vector> #include <algorithm> #include <stack> u...
二叉树的创建和递归与非递归遍历
weixin_33994429的博客
05-18 120
二叉树的创建 //index要给引用！！！ void _Create(Node *&pRoot,T *arr,T invalid,size_t sz,size_t &index) { if (arr[index] != invalid&&index < sz) ...
【数据结构】二叉树的非递归遍历
Changqing9的博客
10-13 301
typedef struct TNode { struct TNode* left; struct TNode* right; int data; }*BinTree; 1、先序遍历 前序遍历按照“根结点-左孩子-右孩子”的顺序进行遍历。 具体算法：先遍历左孩子，并输出。当左孩子遍历完后，取栈顶，并借助栈顶找到右孩子。此时循环还没有结束，再遍历它的左子树，右孩子直至孩子全部遍历结束。 void PreorderTraversal(BinTree T) //前序遍历 { if(!T) ret
二叉树非递归遍历算法实现
"二叉树非递归遍历的C语言实现" 在计算机科学中，二叉树是一种数据结构，由节点（也称为顶点）组成，每个节点最多有两个子节点，通常分为左子节点和右子节点。二叉树遍历是访问二叉树中所有节点的过程，常见的遍历...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值