概率特性仿真实验与程序-Matlab仿真-随机数生成-负指数分布-k阶爱尔兰分布-超指数分布

本文链接：https://blog.csdn.net/sogerno1/article/details/45500795

概率特性仿真实验与程序-Matlab仿真-随机数生成-负指数分布-k阶爱尔兰分布-超指数分布

使用Java中的SecureRandom.nextDouble()生成一个0~1之间的随机浮点数，然后使用反函数法生成一个符合指数分布的随机变量（反函数求得为 $x= -\frac{ln\left ( 1-R \right )}{\lambda }$ ）。指数分布的参数 $\lambda$ 为getExpRandomValue函数中的参数lambda。生成一个指数分布的随机变量的代码如下，后面都将基于该函数生成一组负指数分布、K阶爱尔兰分布、2阶超指数分布随机变量，然后将生成的随机数通过matlab程序进行仿真，对随机数的分布特性进行验证。

public static double getExpRandomValue(double lambda)
{
    return (-1.0/lambda)*Math.log(1-SecureRandom.nextDouble());     
}

生成一组参数为lambda（ $\lambda$ ）的负指数分布的随机变量

通过下面的函数生成一组 $\lambda$ 参数为lambda的随机变量，其中size表示随机变量的个数。通过该函数生成之后，可以将这些随机值保存在文件中，以备分析和验证，比如保存在exp.txt文件中，供下面介绍的matlab程序分析。

    public static double[] genExp(int size, double lambda)
    {
        double[] array = new double[size];
        while(--size>=0) 
        { 
            array[size] = getExpRandomValue(lambda);
        }
        return array;
    }

通过genExp(1000000, 0.2)生成1000000个 $\lambda$ 参数为0.2的随机变量，然后保存到exp.txt中，然后使用下面的matlab程序对这些随机数的性质进行验证，如果这些随机数符合 $\lambda$ =0.2的负指数分布，则其均值应为 $1/\lambda$ ，即1/0.2=5，其方差应为 $1/{\lambda }^{2}=1/(0.2*0.2)=25$ 。然后对这些随机数的概率分布进行统计分析，以长度为1的区间为统计单位，统计各区间内随机数出现的频数，求出在各区间的概率，绘制图形，与参数为 $\lambda$ 的真实负指数分布曲线进行对比。以下为matlab代码。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%测试以λ=0.2为参数的负指数分布
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

randomValues = load ('d:/exp.txt');%从文件导入生成的随机数
X = 1:1:80;%以长度为1的区间为统计单位，统计1~80内的随机数频数

m = mean(randomValues);%计算平均值，如果生成的随机数正确，均值应=1/λ=1/0.2=5
d = var(randomValues);%计算方差，方差应=1/λ^2=1/(0.2^2)=25

all_count = length(randomValues);%随机数个数，方面后面将频数转成概率
[f,xout] = hist(randomValues, X);%按区间统计频数
for i=1:length(X)
    f(i) = f(i)/all_count;%频数转概率
    end;

Y = 0.2*exp(-1*0.2*X);%画出λ=0.2的负指数分布概密函数曲线
plot(X,f,X,Y,'r');%与随机生成的概密函数曲线对比
grid on;%显示格线
legend('统计曲线','实际曲线');%图形注解

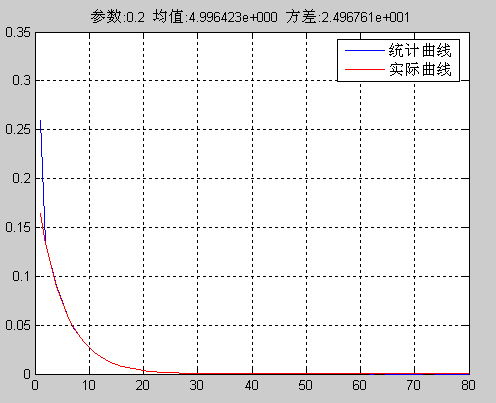
title_str = sprintf('参数:0.2  均值:%d  方差:%d', m, d);
title(title_str);

如下图所示，均值为4.996423，约等于5，方差为24.96761，约等于25，与实际情况相符。此外，通过matlab统计的概率密度函数曲线与真实曲线基本重合（其中在0-1之间没有重合的原因是，实际情况是在0-1之间有无数个点，而matlab统计时以1为一个区间进行统计，只生成了一个统计项，而这无数个点的概率全部加到1点处，因此两条线没有重合，而且1点处的值远大于实际值，如果统计单位划分越细，0-1之间的拟合度更高），表明生成的随机数符合负指数分布。
这里写图片描述

生成一组参数为lambda（ $\lambda$ ）的k阶爱尔兰分布的随机变量

通过下面的函数生成一组 $\lambda$ 参数为lambda的k阶爱尔兰分布随机变量，其中size表示随机变量的个数，k表示阶数。由于k阶爱尔兰分布是k个相同lambda的负指数分布的串联，因此可以将连续k个负指数分布的随机变量相加成为一个爱尔兰分布的随机变量，从而生成爱尔兰分布的随机变量，如下面程序所示。通过该函数生成之后，可以将这些随机值保存在文件中，以备分析和验证，比如保存在erlang_k.txt文件中，供下面介绍的matlab程序分析。

    public static double[] genErlang(int size, double lambda, int k)
    {
        double[] array = new double[size];
        while(--size>=0) 
        { 
            for(int i = 0; i<k; i++)
                array[size] += getExpRandomValue(lambda);
        }
        return array;
    }

通过genErlang(1000000, 0.2, 2)、genErlang(1000000, 0.2, 4)、genErlang(1000000, 0.2, 8)分别生成1000000个 $\lambda$ 参数为0.2的2、4、8阶爱尔兰随机变量，然后分别保存到erlang_2.txt、erlang_4.txt、erlang_8.txt中，然后使用下面的matlab程序对这些随机数的性质进行验证，验证的方法与上面相同，对于k=2，则其均值应为 $k/\lambda$ ，即2/0.2=10，其方差应为 $k/\lambda^2=2/(0.2*0.2)=50$ ；同理，对于k=4，均值应等于20，方差应等于100；对于k=8，均值应等于40，方差应等于200。下图为matlab代码。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%测试以λ=0.2为参数，K分别为2、4、8的爱尔兰分布
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

randomValues_2 = load ('d:/erlang_2.txt');%从文件导入生成的λ=0.2 K=2的随机数
randomValues_4 = load ('d:/erlang_4.txt');%从文件导入生成的λ=0.2 K=4的随机数
randomValues_8 = load ('d:/erlang_8.txt');%从文件导入生成的λ=0.2 K=8的随机数
X = 1:1:80;%以长度为1的区间为统计单位，统计1~80内的随机数频数

m_2 = mean(randomValues_2);%计算平均值，如果生成的随机数正确，均值应=K/λ=2/0.2=10
d_2 = var(randomValues_2);%计算方差，方差应=K/λ^2=2/(0.2^2)=50

m_4 = mean(randomValues_4);%计算平均值，如果生成的随机数正确，均值应=K/λ=4/0.2=20
d_4 = var(randomValues_4);%计算方差，方差应=K/λ^2=4/(0.2^2)=100

m_8 = mean(randomValues_8);%计算平均值，如果生成的随机数正确，均值应=K/λ=8/0.2=40
d_8 = var(randomValues_8);%计算方差，方差应=1/λ^2=8/(0.2^2)=200

all_count_2 = length(randomValues_2);%随机数个数，方面后面将频数转成概率
[f_2,xout_2] = hist(randomValues_2, X);%按区间统计频数
for i=1:length(X)
    f_2(i) = f_2(i)/all_count_2;%频数转概率
    end;

all_count_4 = length(randomValues_4);%随机数个数，方面后面将频数转成概率
[f_4,xout_4] = hist(randomValues_4, X);%按区间统计频数
for i=1:length(X)
    f_4(i) = f_4(i)/all_count_4;%频数转概率
    end;

all_count_8 = length(randomValues_8);%随机数个数，方面后面将频数转成概率
[f_8,xout_8] = hist(randomValues_8, X);%按区间统计频数
for i=1:length(X)
    f_8(i) = f_8(i)/all_count_8;%频数转概率
    end;

plot(X,f_2,'r',X,f_4,'g',X,f_8,'b');

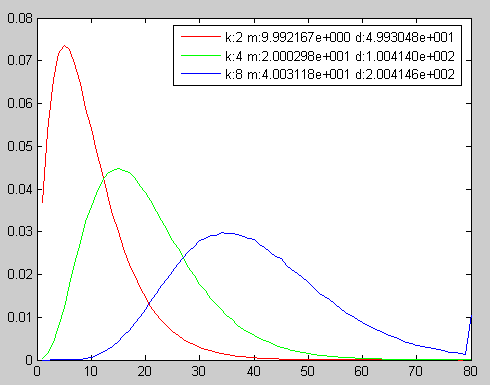
str1 = sprintf('k:2 m:%d d:%d', m_2, d_2);
str2 = sprintf('k:4 m:%d d:%d', m_4, d_4);
str3 = sprintf('k:8 m:%d d:%d', m_8, d_8);
legend(str1,str2,str3); %图形注解

如下图所示，k=2时，均值为9.992167，约等于10，方差为49.93048，约等于50；k=4时，均值为20.00298，约等于20，方差为100.4140，约等于100；k=8时，均值为40.03118，约等于40，方差为200.4146，约等于200，以上结果都与实际情况符合。
这里写图片描述

生成一组2阶超指数分布的随机变量

通过下面的函数生成一组 $\lambda$ 参数分别为lambda1和lambda2的2阶超指数分布随机变量，其中size表示随机变量的个数，lambda1和lambda2表示两个负指数分布的 $\lambda$ 参数，这里指定进入分支1的概率为α1，进入分支2的概率为α2。由于2阶超指数分布是2个 $\lambda$ 参数分别为lambda1和lambda2的负指数分布的并联，且以一定概率进入各分支，因此可以根据概率随机的从两个 $\lambda$ 参数不同的负指数分布中抽取一个随机变量作为一个超指数分布的随机变量，如下面程序所示。通过该函数生成之后，可以将这些随机值保存在文件中，以备分析和验证，比如保存在hyper_exp.txt文件中，供下面介绍的matlab程序分析。

    public static double[] genHyperExp(int size, double lambda1, double lambda2)
    {
        double a1 = 0.3;//a1:进入分支1的概率   因此a2=1-a1=0.7

        double[] array = new double[size];
        while(--size>=0) 
        { 
            if(SecureRandom.nextDouble()>a1)
                array[size] = getExpRandomValue(lambda2);
            else
                array[size] = getExpRandomValue(lambda1);
        }
        return array;
    }

通过genHyperExp(1000000, 0.2, 0.5)生成1000000个参数分别为0.2和0.5，α1=0.3、α2=0.7的超指数分布随机变量，然后保存到hyper_exp.txt中，使用下面的matlab程序对这些随机数的性质进行验证，验证的方法与上面相同，如果生成的随机数正确，均值应=α1/λ1+α2/λ2=0.3/0.2+0.7/0.5=2.9，方差应=2*(α1/λ1^2+α2/λ2^2)-(α1/λ1+α2/λ2)^2=12.19。下图为matlab代码。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%测试λ1=0.2、λ1=0.5、α1=0.3、α2=0.7的2阶超指数分布
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

randomValues = load ('d:/hyper_exp.txt');%从文件导入生成的随机数
X = 1:1:80;%以长度为1的区间为统计单位，统计1~80内的随机数频数

m = mean(randomValues);%计算平均值，如果生成的随机数正确，均值应=α1/λ1+α2/λ2=0.3/0.2+0.7/0.5=2.9
d = var(randomValues);%计算方差，方差应=2*(α1/λ1^2+α2/λ2^2)-(α1/λ1+α2/λ2)^2=12.19

all_count = length(randomValues);%随机数个数，方面后面将频数转成概率
[f,xout] = hist(randomValues, X);%按区间统计频数
for i=1:length(X)
    f(i) = f(i)/all_count;%频数转概率
    end;

plot(X,f);
grid on; % 显示格线
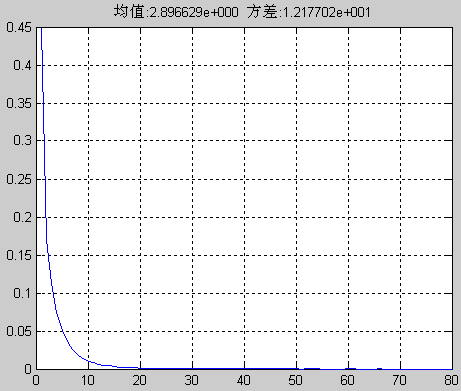
title_str = sprintf('均值:%d  方差:%d', m, d);
title(title_str);