什么是线性基?
先来回顾一下向量空间中的基。这个基代表着空间的一个极大线性无关子集,组中向量线性无关,且空间中的任意一个向量都可以唯一地由基中的向量来表示
那么回到线性基,它其实就类似于是一个向量空间的基
我们考虑一个问题:给定一个数组a,要求一个最小的数组d,使得a中的任意一个数可以由d中的若干个数字来通过异或得到,且d中任意多个数字的异或结果不为0
注意到异或操作其实就是在模2意义下的加法操作,我们如果将每一个数字按二进制位分解,就可以看成一个n维向量(我们假定数字<=2^n)
所以当前要求的东西如下:
给定一个向量组a,,求一组向量d,
(向量个数为m),使得
,存在唯一的一组解k满足
(加法在模2意义下),且不存在一组解s,使得
.
这里
(事实上这样一个线性基不一定是原数组的子集,但是略去这一点的话,它跟空间中的基的概念就有诸多相像的地方了。
这里列出对应的性质
1.数组中的任意一个数可以唯一地由线性基中的若干元素异或得到
2.线性基中任意多个元素的异或值不为0
3.线性基元素的异或集合等于原数组元素的异或集合
那么我们考虑一下如何求出这样一个集合并满足上述性质
好吧其实我也不知道前人是怎么搞出来这个东西的,但是可以意会一下
异或中一个极好的思考角度就是从二进制位入手。想要得到一个数字,说白了就是要让对应位为1或0.那么如果我们的线性基中,每一个数字都有一位,满足其它数字在这一位上都是0,那么或许就可以操控了。所以线性基其实就是按位分成n个数字,每一位对应一个数字(或许没有)
这里先给出求线性基的代码,再慢慢讲解(很简单的,别走)
void add(ll x)
{
for(int i=63;i>=0;--i)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
}这是一个将元素尝试添加进线性基的代码。我们的操作就是,让线性基中每一个元素的最高位拥有唯一的1,就没了。这里如果一个数组的某一个1位已经存在对应的线性基元素了,我们直接将其取异或,知道它的最高位1是唯一的。如果没有这样的位,也就是最后x=0,就无法加入线性基
为什么这样是合理的?我们一个性质一个性质来看
不妨先看性质2 线性基中任意多个元素的异或值不为0
我们假设d[a]^d[b]^d[c]=0,并假设三者加入线性基的次序是a,b,c
显然d[a]^d[b]=d[c],所以在c尝试加入线性基的时候,就会加入失败。
得证
再看性质1 数组中的任意一个数可以唯一地由线性基中的若干元素异或得到
先考虑可行性:
假设数字A成功加入线性基的第i个位置
那么A^d[a]^d[b]^...^d[c]=d[i],反过来:A=d[a]^d[b]^...^d[c]^d[i].
如果A没有加入线性基
那就是因为线性基中存在一些数字的异或和=A
得证
再考虑唯一性:
如果存在两种方案使得d[a1]^d[a2]^..d[ai]=d[b1]^d[b2]^..d[bj]=A,那么取d[a1]^d[a2]^..d[ai]^d[b1]^d[b2]^..d[bj]=0,与性质2矛盾
得证
性质3 线性基元素的异或集合等于原数组元素的异或集合
线性基中的元素都是原数组元素互相异或得来的,所以该性质显然
所以说这样构造是合理的,其实就是按位贪心。
然后我们考虑一下用处:
求数组异或最大值
ans=0;
for(int i=60;i>=0;--i)
{
ans=max(ans,ans^d[i]);
}其实还是按位贪心,如果高位能取到1的话,就取,因为决策具有单调性。
求数组异或最小值
如果有元素不能插入线性基,那么最小值显然就是0,否则就是线性基里最小的元素,因为最小的元素无论异或谁都会变大
求数组异或的第k小
我们考虑将线性基重新构造,使得每一个数字的每一位1都是唯一的
如果i<j,aj的第i位是1,就将aj异或上ai。
这样,我们只需要将k按二进制拆分,对于1的位,就异或上对应的元素即可
例题
求数组异或最大值
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,k;
ll mas[N];
ll d[70];
void add(ll x)
{
for(int i=60;i>=0;--i)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>mas[i];
for(int i=1;i<=n;++i) add(mas[i]);
ll ans=0;
for(int i=60;i>=0;--i)
{
ans=max(ans,ans^d[i]);
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//ll t;cin>>t;while(t--)
solve();
return 0;
}大意:
求数组的异或结果的种类数
思路:
我们考虑性质2,显然线性基中不同元素的异或结果一定不同,所以答案就是2^(线性基大小)
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
string s;
ll d[70];
vector<ll> vt;
void add(ll x)
{
for(int i=60;i>=0;--i)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=m;++i)
{
cin>>s;
ll cnt=0;
for(int j=0;j<n;++j)
{
cnt*=2ll;
if(s[j]=='O') cnt++;
}
//cout<<cnt<<endl;
vt.push_back(cnt);
}
for(auto i:vt) add(i);
ll num=0;
for(int i=0;i<=60;++i) if(d[i]>0) num++;
ll ans=1;
for(int i=1;i<=num;++i)
{
ans=ans*2%2008;
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}大意:
每一个元素有一个id和val,选择一个子集,任意多个id的异或结果不为0,且val最大
思路:
线性基中任意元素的异或结果不为0,所以其实就是要求一个val最大的线性基。那么我们只要按val倒序贪心即可
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
struct ty
{
ll num,val;
}mas[N],d[70];
bool cmp(ty a,ty b)
{
return a.val>b.val;
}
void add(ty a)
{
for(int i=60;i>=0;--i)
{
if(a.num&(1ll<<i))
{
if(d[i].num)
{
a.num^=d[i].num;
// a.val+=d[i].val;
}
else
{
d[i]=a;
break;
}
}
}
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i)
{
cin>>mas[i].num>>mas[i].val;
}
sort(mas+1,mas+1+n,cmp);
for(int i=1;i<=n;++i) add(mas[i]);
ll sum=0;
// cout<<"sdf "<<endl;
// for(int i=0;i<=60;++i) if(d[i].num) cout<<d[i].num<<" "<<d[i].val<<endl;
// cout<<endl;
for(int i=0;i<=60;++i) sum+=d[i].val;
cout<<sum<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}大意:
(懒
思路:
Nim的一个结论就是元素异或和为0时,先手必败,否则先手必胜
所以当前先手的策略就是使得后手无论怎么拿,都不可能使元素异或和=0。也就是,我们要取尽可能少的数,使得局面成为一个线性基。因为总能构造出一个线性基(多了就拿掉呗),所以先手必胜
那么升序插入线性基即可
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
ll mas[N];
ll d[70];
ll sum=0;
void add(ll x)
{
ll pre=x;
for(int i=60;i>=0;--i)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
if(x==0) sum+=pre;
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>mas[i];
sort(mas+1,mas+1+n,greater<ll>());
for(int i=1;i<=n;++i) add(mas[i]);
cout<<sum<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}大意:
给一个 n 个点 m 条边(权值为di)的无向有权图,可能有重边和子环。可以多次经过一条边,求1→n 的路径的最大边权异或和。
思路:
显然,一条边被走两次之后,贡献就是0,那么我们什么时候会这样做?当第二次经过时可以到达其它地方时
其实这里有一类边集是很特殊的,环。我们可以异或来得到整个环的值,再从起点出去,就类似于是一个额外贡献。
这启示我们,我们可以将图分为一个一个环和一条链。我们的主线是链,我们沿着链走,中间碰到有环可以走的话,我们可以走,也可以不走。那么就相当于求环的值的集合的一个线性基,然后求链的值与该线性基元素的异或的最大值即可。
这里还有两个问题:
1.从环回去要走重边,所以环的值要扣掉重边对应的部分
2.如何选择我们的主链?
事实上,如果有两条主链的话,就有了一个环
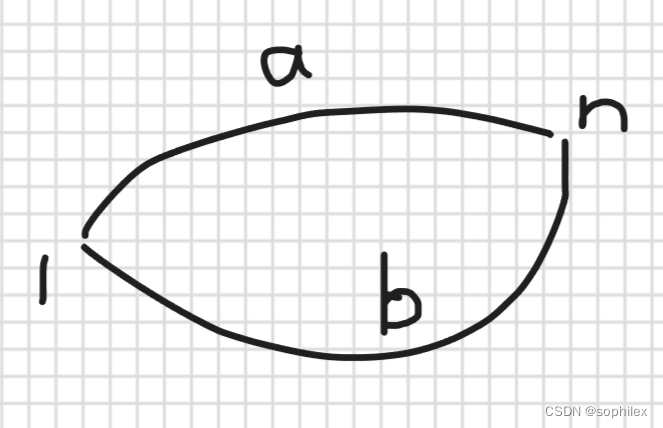
我们取价值为a的路,可能不如b优,但是环的价值是a^b,那么在最后的操作中,a^(a^b),就得到了b。所以我们其实可以任意选择一开始的主链。另外,选择不同的主链,最后可能会得到不同的一个一个的环。如何保证不同链能得到相同的环?不能保证,环套环的情况可能会导致不同的遍历顺序得到不同的环,但是简单环的异或操作可以得到所有的简单环。具体可以看一下这里
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
struct ty
{
ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
ll res[N];
ll vis[N];
ll d[70];
void add(ll x)
{
for(int i=63;i>=0;--i)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
}
ll ma(ll x)
{
ll ans=x;
for(int i=63;i>=0;--i)
{
ans=max(ans,ans^d[i]);
}
return ans;
}
void add(ll a,ll b,ll c)
{
edge[++cn].t=b;
edge[cn].l=c;
edge[cn].next=head[a];
head[a]=cn;
}
void dfs(ll id,ll now)
{
vis[id]=1;res[id]=now;
for(int i=head[id];i!=-1;i=edge[i].next)
{
ll y=edge[i].t;
if(!vis[y]) dfs(y,now^edge[i].l);
else add(now^edge[i].l^res[y]);
}
}
void solve()
{
memset(head,-1,sizeof head);
cin>>n>>m;
for(int i=1;i<=m;++i)
{
ll a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
dfs(1,0);
// for(int i=64;i>=0;--i) if(d[i]) cout<<d[i]<<' ';
// cout<<endl;
cout<<ma(res[n])<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}大意:
跟上一题一样,只是变成求路径异或最小值了
那么只是换个板子的事情
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
struct ty
{
ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
ll res[N];
ll vis[N];
ll d[70];
void add(ll x)
{
for(int i=63;i>=0;--i)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
}
ll mi(ll x)
{
ll ans=x;
for(int i=63;i>=0;--i)
{
ans=min(ans,ans^d[i]);
}
return ans;
}
void add(ll a,ll b,ll c)
{
edge[++cn].t=b;
edge[cn].l=c;
edge[cn].next=head[a];
head[a]=cn;
}
void dfs(ll id,ll now)
{
vis[id]=1;res[id]=now;
for(int i=head[id];i!=-1;i=edge[i].next)
{
ll y=edge[i].t;
if(!vis[y]) dfs(y,now^edge[i].l);
else add(now^edge[i].l^res[y]);
}
}
void solve()
{//1<<64就炸了
memset(head,-1,sizeof head);
cin>>n>>m;
for(int i=1;i<=m;++i)
{
ll a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
dfs(1,0);
// for(int i=64;i>=0;--i) if(d[i]) cout<<d[i]<<' ';
// cout<<endl;
cout<<mi(res[n])<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}大意:
求一组向量的极大无关组,其中每一个向量还有一个价值val,要求极大无关组的val总和最小
思路:
其实就是实数意义下的一个线性基。那么我们用高斯消元,像求线性基一样,如果当前最高位(向量最左边元素)没有对应的线性基,就加入,并更新后面对应的元素即可
至于val总和最小,跟之前一样,贪心即可
其实就是一个消元求解方程组的过程。
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define ldb long double
const ldb eps=1e-7;
const ll N=510;
ll n,m;
struct ty
{
ldb val[N];
ldb cost;
friend inline bool operator <(const ty& a,const ty& b)
{
return a.cost<b.cost;
}
}mas[N];
ll d[N];
ll cnt=0;
ldb ans=0;
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j) cin>>mas[i].val[j];
}
for(int i=1;i<=n;++i) cin>>mas[i].cost;
sort(mas+1,mas+1+n);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
if(abs(mas[i].val[j])<eps) continue;
if(!d[j])
{
d[j]=i;//确定对应的基
ans+=mas[i].cost;
cnt++;
break;
}
ldb ap=mas[i].val[j]/mas[d[j]].val[j];
for(int k=j;k<=m;++k)
{
mas[i].val[k]-=ap*mas[d[j]].val[k];
}
}
}
cout<<cnt<<' '<<(ll)ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}未完待续~






















 248
248











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








