符号计算两大商业化顶级软件;
maple刚刚出了 19 (公开叫2015), mathematica也有了10.x
看了下,感觉网上有很多人视图对比不同软件,这个比较更加贴近实际情况.因此转发下;
因为楼主在日本留学,学校和三个公司都签了约。所以电脑里matlab,mathematica,Maple都有。matlab是数值计算,矩阵计算最好已经不用说了。但·mathematics和Maple到底哪个好,一直有疑点。看了这篇比较后,我的疑点被解开了。
https://sites.google.com/site/yoshihikohasegawa/adversaria
这篇是东京大学的教授写的Maple18和mathematica9的详细比较
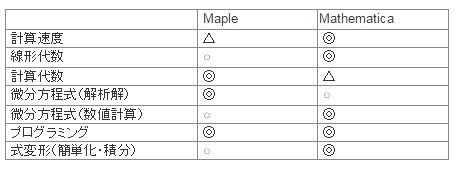
上表中的日文可以直接看作繁体汉字的一种; 全是假名的一行指"编程语言"programming language
以上是综合评价, 三角表示"马马虎虎",单圈代表"挺不错的",双圈代表"非常出色";
符号计算
记号计算の主な使用目的は积分,简単化,微分方程式等だと思われます.积分はMathematicaの方が强力な印象があります.例えばx*exp(-x)*exp(-exp(-x))
をxに関して积分する场合,Mathematicaだと解析解が一発で计算されますがMapleだとそのままでは计算できません.Mapleで计算する场合は置换积分を行うと出来ます.
f:=Int(x*exp(-x)*exp(-exp(-x)),x);
g:=IntegrationTools:-Change(f,x=-ln(u));
value(g);
=> -ln(u)*exp(-u)-Ei(1,u)
また,式の简単化に関してもMathematicaの方が强力です.
一方で,微分方程式の解析解はMapleの方がより広い场合で计算が可能なようです.例えば,
y*(x)-y(x)^2-y(x)*sin(2*x)-cos(2*x)=0
をMapleとMathematicaで解いた场合,Mapleでは
y(x)=(2*HeunCPrime(1,1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)*_C1*cos(2*x)/(sqrt(2*cos(2*x)+2)*(HeunC(1,1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)*_C1*sqrt(2*cos(2*x)+2)+HeunC(1,-1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)))+(HeunCPrime(1,-1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)*sqrt(2*cos(2*x)+2)+2*HeunCPrime(1,1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)*_C1+2*HeunC(1,1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)*_C1)/(sqrt(2*cos(2*x)+2)*(HeunC(1,1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2)*_C1*sqrt(2*cos(2*x)+2)+HeunC(1,-1/2,-1/2,-1,7/8,(1/2)*cos(2*x)+1/2))))*sin(2*x);
という解が得られますが,Mathematicaでは解くことが出来ません.文献[数式処理 Bulletin of JSSAC (2012), Vol.18, pp.117-125]によれば,Kamkeの本に载っている微分方程式の97%以上を解くことが出来るそうです.
また积分方程式に関してはMapleの方が强力です.Mapleにはintsolveという専用の関数が用意されており,これによって解析解を计算することが可能です.例えばeq:=f(x)=2*x^2-x+Int(f(t),t=0..2)のf(x)に関する积分方程式をMapleで解くとintsolve(eq,f(x)) => 2*x^2-x-10/3となり,解析的に解を求めることが出来ます.一方,Mathematicaには积分方程式用のコマンドは用意されていないため,直接解くことは出来ません.
总体内容 :积分是mathematica强,化简也是mathematica的强项。有些mathematica可以直接积分的,Maple却要用置换积分。微分方程的解析解是Maple强些,有很多微分方程的解析解Maple能算出,mathematica却不能。根据文献,Maple可以解Kamke书上的97%的微分方程。
另外,积分方程也是Maple强些,因为Maple里内带intsolve函数,因此可以算出解析解。例如eq:=f(x)=2*x^2-x+Int(f(t),t=0..2)的关于f(x)的积分方程,Maple得出intsolve(eq,f(x)) => 2*x^2-x-10/3,而Mathematica解不了。
数値计算
数値计算は全体的にMathematicaの方が処理が高速です.数値计算では,目的関数の最大化最小化を求める问题が非常に多いですが,そのコマンドもMathematicaの方が多いようです.例えば,大域的最适解を求めるためにMathematicaでは,焼きなまし法,Differential evolution,マルチスタートHill climbingが组み込み関数で入っています(NMaximizeまたはNMinimize関数).一方で,Mapleではこれらの手法はアドインとして贩売されており,组み込み関数ではNLPSolveが提供されているだけです.线形计画法はどちらも,记号的に条件を入力できます(行列による入力ももちろん可能).しかし,大规模な问题はどちらのソフトも得意ではなく,GLPKと比べても大きく见劣りする印象です.
数値积分はdefaultの関数を用いる场合Mathematicaの方が高速です.しかし,Mapleで明示的にNAGのライブラリを指定することで,Mathematicaより高速に数値积分をすることもできます.常微分方程式の机能に関しては,MathematicaもMapleも概ね同等の机能を有しています.阳解法と阴解法を有しており,硬い微分方程式も解くことが出来ます.但し,时间遅れのある微分方程式の数値解に関しては,Mathematicaのみが解くことが出来ます.また确率微分方程式に関しても,Mathematicaはバージョン9より数値的に解くための(モンテカルロ法)関数が追加されました.一方で,Mapleには确率微分方程式のパッケージは入っていません.
保存量(エネルギーや运动量)を持つ微分方程式は微分代数方程式(Differential Algebraic Equation)と呼ばれますが,どちらのソフトでも解くことが出来ます.机能はMathematicaの方が揃っている印象です.
总体内容:数值计算是mathematica好,主要差别在于有时间差的微分方程的数值解只有mathematical可以解,再者从mathematica9开始可以解概率微分方程了,Maple还不行。总体来说mathematica在这个方面比Maple强。
プログラミング言语··(Programming language)
Mathematicaは関数型言语である一方,MapleはC言语に似ている一般的な手続き型言语です.言语としてはMathematicaの方が洗练されていて,プログラムを非常に少ない行数でエレガントに记述することが可能です.一方,Mapleは互换性を持たせつつ拡张を重ねているため,复雑になっています(特にデータ构造).Mapleは最近ではObject指向にも対応しています.ただし,论文にある拟コードは手続型であるために,简単にプログラミングする场合はMapleの方がしやすいです.また,C言语やMATLABソースの移植を行う场合も,これらの言语と文法が似ているのでMapleの方が圧倒的に简単に出来ます.中规模以上のプログラミングではモジュール化が重要ですが,これもMapleの方が行いやすいです.MathematicaではContextを指定することで名前空间を指定できますが,コーディングには手间がかかります.また,エラー処理に関してもMapleの方が行いやすく,个人的にはプログラミングはMapleの方が简単に出来る印象です.私自身はMapleの方がMathematicaより频繁に使いますが,その大きな理由の一つがこのプログラミング机能にあります.
总体内容: 由于Maple像C语言,Maple比mathematica简单,matlab移植也是Maple比mathematica强多了。
线性代数
线形代数の机能はMathematicaの方が高机能です.例えば疎行列の固有値を求める场合,最大・最小の固有値のみを计算したい场合がありますが,Mapleでは固有値の一部のみの计算を行うことが出来ません.一方Mathematicaは内部でARPACK使っていて,Eigenvaluesコマンドで行うことが出来ます.大规模な疎行列の计算もMathematicaの方が高速です.特にMathematicaの疎行列はC言语などで书いた场合とそん色なく计算できる场合があります.
总体内容: 线性代数是mathematica强,有些Maple不能做的mathematica能做,再者mathematics比Maple快。
计算代数几何
MapleやMathematicaなどの记号计算ソフトを用いる大きな理由の一つに,代数系の计算が挙げられます.数値计算,プログラミング,大规模线形代数が主であれば,おそらくMATLABなどの数値计算専用のソフトの方が良いでしょう.そのため,代数系の计算は数式処理ソフトにとって非常に重要です.Mapleの开発には计算代数の研究者が参加しているため,计算代数の机能はMathematicaと比较して圧倒的に豊富です.特にイデアルの操作を行うPolynomialIdealsパッケージのコマンドのほとんどはMathematicaにはありません.例えば,イデアルの和,积,共通部分,コロンイデアル,根基イデアルなどの计算はMathematicaでは出来ません.多项式自体の计算もMapleの方が高速です.また微分多元环に関するコマンドもMathematicaにはないです.代数の计算を行うならばMapleの方がだいぶ适している印象です.
总体内容:计算代数是Maple的超强项,强暴于mathematica,特别是PolynomialIdeals操作等,微分多元环操作mathematica是没有的,再者多项式计算也是Maple快于mathematica。所以,代数计算是Maple大大超过mathematica。
GUI·(Graphic Uesr Interface)
GUIは机能ではありませんが,非常に重要です.MathematicaはCourierベースのフォントを用いており,プログラミングと数学的记号の表现を出来るように工夫されています.一方,MapleはTimesベースのフォントが使われており,见た目はLatexのような非常に绮丽な表示が可能です.プログラミングを行うにはMathematicaのGUIの方が向いていますが,记号计算にはMapleのほうが数学的です.ただしMapleにはプログラミングのためのコードエディタを埋め込むことが可能です.
总体内容 Maple的GUI像LATEX一样漂亮,而Mathematica适应于编程GUI
总结下: 仁者见仁智者见智
Maple和mathematica都得用,微分,积分方程基本可以拜托Maple了(概率微分方程拜托mathematica)。
积分拜托给mathematica。 计算代数几何,GUI,Programming拜托给Maple。
线性代数,数值计算拜托给matlab和mathematica。
























 3666
3666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








