单调栈题目：最大矩形

题目

标题和出处

标题：最大矩形

出处：85. 最大矩形

难度

8 级

题目描述

要求

给定一个仅包含 $\text{0}$ 和 $\text{1}$、大小为 $\text{rows}\times \text{cols}$ 的二进制矩阵 $\text{matrix}$，找出只包含 $\text{1}$ 的最大矩形，并返回其面积。

示例

示例 1：

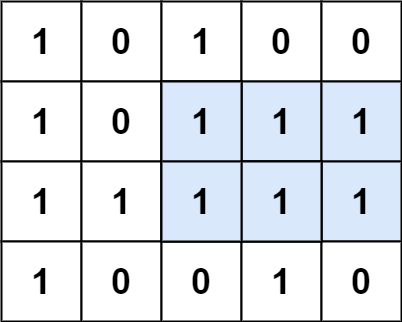
输入：$\text{matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]}$
输出：$\text{6}$
解释：最大矩形如上图所示。

示例 2：

输入：$\text{matrix = []}$
输出：$\text{0}$

示例 3：

输入：$\text{matrix = [["0"]]}$
输出：$\text{0}$

示例 4：

输入：$\text{matrix = [["1"]]}$
输出：$\text{1}$

示例 5：

输入：$\text{matrix = [["0","0"]]}$
输出：$\text{0}$

数据范围

• $\text{rows}=\text{matrix.length}$
• $\text{cols}=\text{matrix[0].length}$
• $\text{0}\le \text{row, cols}\le \text{200}$
• $\text{matrix[i][j]}$ 为 $\text{‘0’}$ 或 $\text{‘1’}$

解法

思路和算法

只要记录矩阵中的每个元素 $1$ 及其上边的连续 $1$ 的数量，即可使用「柱状图中最大的矩形」的方法求解。具体而言，创建一个和 $\text{matrix}$ 相同大小的矩阵，新矩阵中的每个元素为 $\text{matrix}$ 中相同位置的元素及其上边的连续 $1$ 的数量，特别地，对于 $\text{matrix}$ 中的元素 $0$，新矩阵中的对应元素是 $0$。

示例 1 的 $\text{matrix}$ 如下：

$$\begin{array}{ccccc}1& 0& 1& 0& 0\\ 1& 0& 1& 1& 1\\ 1& 1& 1& 1& 1\\ 1& 0& 0& 1& 0\end{array}$$

对应的新矩阵如下：

$$\begin{array}{ccccc}1& 0& 1& 0& 0\\ 2& 0& 2& 1& 1\\ 3& 1& 3& 2& 2\\ 4& 0& 0& 3& 0\end{array}$$

对于新矩阵中的每一行，其中的元素可以看成是以这一行为底的柱状图的每个柱子的高度。因此，在计算出新矩阵之后，遍历新矩阵的每一行，使用「柱状图中最大的矩形」的方法计算以这一行为底的最大矩形面积，遍历全部行之后即可得到矩阵中只包含 $1$ 的最大矩形面积。

实现方面，并不需要事先计算出新矩阵，而是可以在遍历 $\text{matrix}$ 的过程中计算，每次计算一行。

具体做法是，创建长度为 $\text{cols}$ 的数组 $\text{heights}$，初始时 $\text{heights}$ 的每个元素都是 $0$，依次遍历 $\text{matrix}$ 的每一行，进行如下操作：

1. 对于 $\text{matrix}$ 的当前行的每个元素，如果该元素是 $0$ 则将 $\text{heights}$ 的对应元素设为 $0$，如果该元素是 $1$ 则将 $\text{heights}$ 的对应元素加 $1$，此时 $\text{heights}$ 的每个元素为 $\text{matrix}$ 中的对应位置的元素及其上边的连续 $1$ 的数量；

2. 遍历完 $\text{matrix}$ 的当前行之后，根据 $\text{heights}$ 计算以当前行为底的最大矩形面积，并更新结果。

遍历结束之后返回结果。

代码

class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int maxArea = 0;
        int rows = matrix.length, cols = matrix[0].length;
        int[] heights = new int[cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (matrix[i][j] == '0') {
                    heights[j] = 0;
                } else {
                    heights[j]++;
                }
            }
            maxArea = Math.max(maxArea, getMaxArea(heights));
        }
        return maxArea;
    }

    public int getMaxArea(int[] heights) {
        int length = heights.length;
        int[] left = new int[length];
        int[] right = new int[length];
        Arrays.fill(left, -1);
        Arrays.fill(right, length);
        Deque<Integer> stack = new ArrayDeque<Integer>();
        for (int i = 0; i < length; i++) {
            int height = heights[i];
            while (!stack.isEmpty() && heights[stack.peek()] >= height) {
                right[stack.pop()] = i;
            }
            if (!stack.isEmpty()) {
                left[i] = stack.peek();
            }
            stack.push(i);
        }
        int area = 0;
        for (int i = 0; i < length; i++) {
            area = Math.max(area, (right[i] - left[i] - 1) * heights[i]);
        }
        return area;
    }
}

复杂度分析

• 时间复杂度：$O(\text{rows}\times \text{cols})$，其中 $\text{rows}$ 和 $\text{cols}$ 分别是矩阵 $\text{matrix}$ 的行数和列数。需要遍历矩阵 $\text{matrix}$ 的每一行，行数是 $\text{rows}$，对于每一行，计算 $\text{heights}$ 和计算以这一行为底的最大矩形面积的时间复杂度都是 $O(\text{cols})$，因此总时间复杂度是 $O(\text{rows}\times \text{cols})$。

• 空间复杂度：$O(\text{cols})$，其中 $\text{cols}$ 是矩阵 $\text{matrix}$ 的列数。数组 $\text{heights}$ 的长度是 $\text{cols}$，计算以每一行为底的最大矩形面积的空间复杂度是 $O(\text{cols})$，因此总空间复杂度是 $O(\text{cols})$。