二叉树的创建、添加和遍历
- 因为我之前文章>>>二叉树详解 已经详细写了二叉树的创建以及二叉树的广度和深度遍历,这里就不重复叙述实现过程,直接将代码规范书写如下:
class TreeNote(object): # 创建树的结点
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object): # 创建二叉树
def __init__(self):
self.root = None # 根结点
def add(self, val): # 二叉树添加结点
node = TreeNote(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def bre_order(self, node): # 二叉树的广度遍历
if node is None:
return
queue = [node]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, end=" ")
if temp_node.left is not None:
queue.append(temp_node.left)
if temp_node.right is not None:
queue.append(temp_node.right)
'''递归实现二叉树的三种深度遍历'''
# def pre_order(self, node): # 二叉树的前序遍历(递归)
# if node is None:
# return
# print(node.val, end=" ")
# self.pre_order(node.left)
# self.pre_order(node.right)
#
# def in_order(self, node): # 二叉树的中序遍历(递归)
# if node is None:
# return
# self.in_order(node.left)
# print(node.val, end=" ")
# self.in_order(node.right)
#
# def post_order(self, node): # 二叉树的后序遍历(递归)
# if node is None:
# return
# self.post_order(node.left)
# self.post_order(node.right)
# print(node.val, end=" ")
'''非递归实现二叉树的三种深度遍历'''
def pre_order(self, node):
if node is None:
return
stack = []
temp_node = node
while temp_node or stack:
while temp_node:
print(temp_node.val, end=" ")
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
temp_node = node.right
def in_order(self, node):
if node is None:
return
stack = []
temp_node = node
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
print(node.val, end=" ")
temp_node = node.right
def post_order(self, node): # 二叉树的后序遍历(非递归)
if node is None:
return None
stack = []
temp_node = node
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
left_node = stack[-1]
temp_node = left_node.right
if temp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
print("\n广度遍历为:")
t.bre_order(t.root)
print("\n前序遍历为:")
t.pre_order(t.root)
print("\n中序遍历为:")
t.in_order(t.root)
print("\n后序遍历为:")
t.post_order(t.root)
'''
广度遍历为:
0 1 2 3 4 5 6 7 8 9
前序遍历为:
0 1 3 7 8 4 9 2 5 6
中序遍历为:
7 3 8 1 9 4 0 5 2 6
后序遍历为:
7 8 3 9 4 1 5 6 2 0
'''
二叉树的查找与修改
查找指定元素的父结点
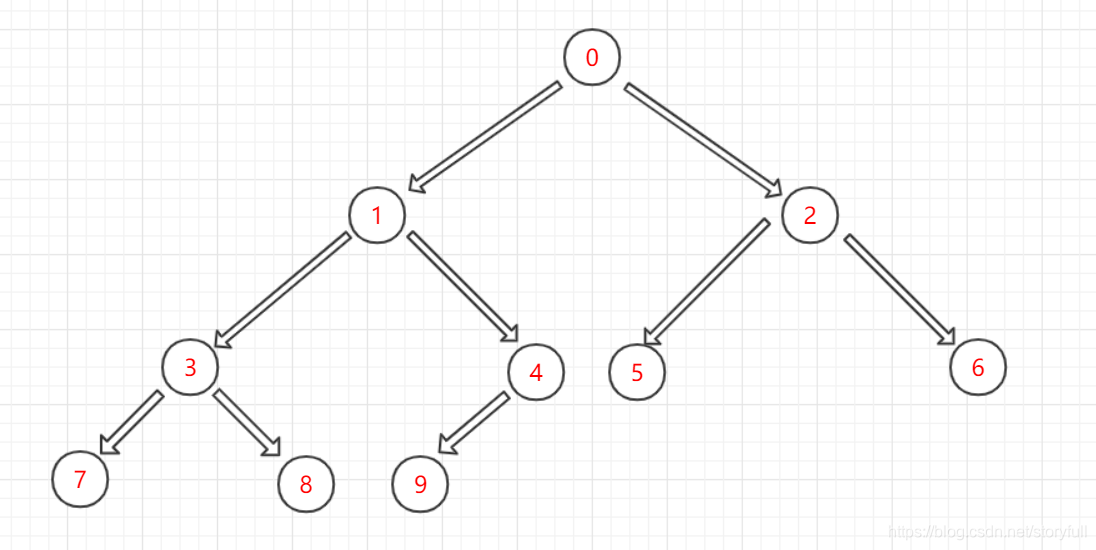
- 还是以为这下图为例,我们先来实现如何查找到给定值的父结点
- 整体思路用的是广度遍历,一层一层的去判断,并添加每一个结点的左右子结点,然后重复判断
class TreeNode(object):
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
def add(self, val): # 添加结点
node = TreeNode(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def get_parent(self, val): # 二叉树查找父结点
if self.root.val == val: # 根结点没有父结点
return None
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left and temp_node.left.val == val:
return temp_node
if temp_node.right and temp_node.right.val == val:
return temp_node
if temp_node.left:
queue.append(temp_node.left)
if temp_node.right:
queue.append(temp_node.right)
return None
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
print(t.get_parent(2).val) # 如要查找值为2的结点的父结点,结果为 0 即是根结点
查找指定值/结点、修改指定值/结点
- 分别用广度、深度三种方式来实现查找指定值,如果找到则返回该结点,并打印该结点值,没找到则返回空
- 分别测试查找一个指定值,所花费的次数,注意测试次数和选定的结点数值位置有关
class TreeNode(object):
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
def add(self, val): # 添加结点
node = TreeNode(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def bre_search(self, val): # 二叉树广度查找
print("进入广度查找") # 进入,需要直接比较根结点
if self.root.val == val:
return self.root
queue = [self.root]
while queue:
temp_node = queue.pop(0)
print("进入广度查找") # 注意计算比较次数的位置
if temp_node.left and temp_node.left.val == val:
return temp_node.left
print("进入广度查找") # 第二条分支也应当有一个
if temp_node.right and temp_node.right.val == val:
return temp_node.right
if temp_node.left:
queue.append(temp_node.left)
if temp_node.right:
queue.append(temp_node.right)
return None
def pre_search(self, node, val): # 二叉树前序查找(递归)
if node is None:
return
print("进入前序查找") # 比较次数进入位置
if node.val == val:
return node
left_part = self.pre_search(node.left, val)
if left_part:
return left_part
right_part = self.pre_search(node.right, val)
if right_part:
return right_part
return None
def in_search(self, node, val): # 二叉树中序查找(递归)
if node is None:
return
left_part = self.in_search(node.left, val)
if left_part:
return left_part
print("进入中序查找") # 从这里开始计算比较
if node.val == val:
return node
right_part = self.in_search(node.right, val)
if right_part:
return right_part
return None
def post_search(self, node, val): # 二叉树后序查找(递归)
if node is None:
return
left_part = self.post_search(node.left, val)
if left_part:
return left_part
right_part = self.post_search(node.right, val)
if right_part:
return right_part
print("进入后序查找") # 从这里开始计算比较
if node.val == val:
return node
return None
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
# 广度查找
bre_res = t.bre_search(4)
if bre_res:
print(bre_res.val)
else:
print(bre_res)
# 前序查找
pre_res = t.pre_search(t.root, 4)
if pre_res:
print(pre_res.val)
else:
print(pre_res)
# 中序查找
in_res = t.in_search(t.root, 4)
if in_res:
print(in_res.val)
else:
print(in_res)
# 后序查找
post_res = t.post_search(t.root, 4)
if post_res:
print(post_res.val)
else:
print(post_res)
'''输出结果:
进入广度查找
进入广度查找
进入广度查找
进入广度查找
进入广度查找
4
进入前序查找
进入前序查找
进入前序查找
进入前序查找
进入前序查找
进入前序查找
4
进入中序查找
进入中序查找
进入中序查找
进入中序查找
进入中序查找
进入中序查找
4
进入后序查找
进入后序查找
进入后序查找
进入后序查找
进入后序查找
4
'''
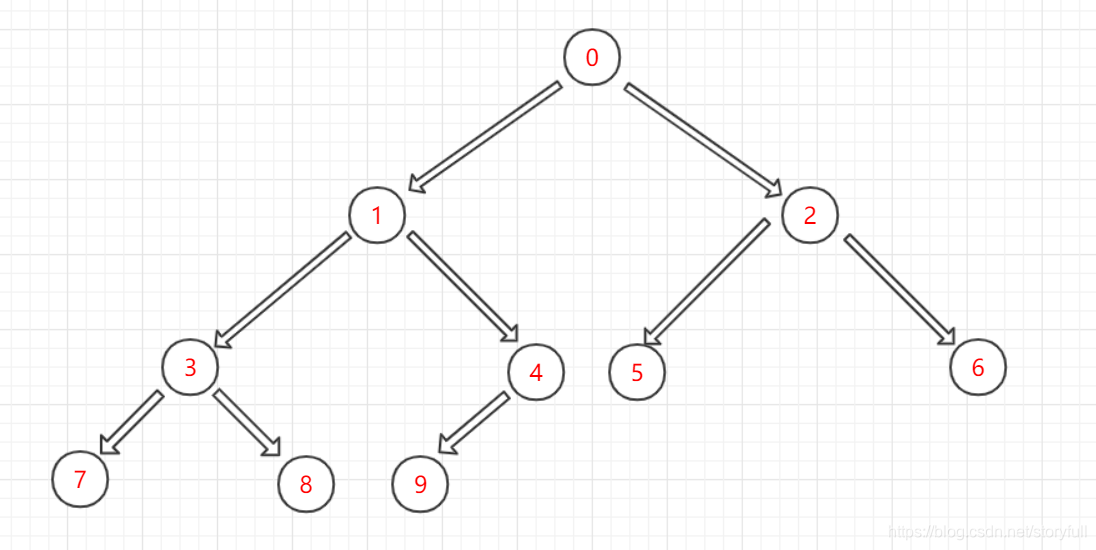
- 上述示例以查找结点4值为4,比较四种遍历方式所花费次数,广度遍历 依次为:[0,1,2,3,4] 所以是5次,分别在根结点,左右子结点处发生比较;前序遍历依 次为[0,1,3,7,8,4] 所以是6次;中序遍历 依次为:[7,3,8,1,9,4] 所以是6次;后序遍历 依次为:[7,8,3,9,4] 所以是5次,可以对比下图,去验证一下!

- 关于二叉树的修改和二叉树查找原理是一样的,只需要用四种查找方式的一种先找到要修改的结点,然后返回该结点,把新的值赋值给该结点的val就可以了,这里就不加赘述了!
二叉树的删除
-
二叉树的删除,真正的操作是在二叉搜索树的基础上来实现的,至于二叉搜索树(二叉排序树)的删除会另开文章详解
-
这里仅叙述二叉树如何删除节点,而且规定:
-
如要要删除非叶子结点,就把它的左右子树都删除,即:如果要删的不是非叶子结点,删除它就连同它的左右子树一起删除;这是因为二叉树通常“指向”都是从根指向叶子,只能去找它的左右子树结点,而无法去找它的“根结点”(下面这种情况,通过写一个方式可以找各个“根结点”);这种情况用递归能很好完成!
class TreeNode(object):
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
self.flag = False # 主函数输出判断
def add(self, val): # 添加结点
node = TreeNode(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def pre_oreder(self, node): # 用前序遍历来测试 删除前和删除后的数据
if node is None:
return
stack = []
temp_node = node
while temp_node or stack:
while temp_node:
print(temp_node.val, end=" ")
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop(-1)
temp_node = node.right
def del_val(self, node, val):
if node is None:
return
if node.val == val and node == self.root: # 如果删除的是根结点,直接置空,然后退出
self.root = None
return
if node.val == val: # 找到了该结点,将当前结点左右置空,然后返回该结点的值
node.left = None
node.right = None
return node.val # 返回结点值来提供判断条件,如果有返回值,说明找到了,没有则没找到
left_part = self.del_val(node.left, val)
if left_part: # 如果左侧有返回值,说明找到了,将当前层的结点的左侧置为空即可
self.flag = True
node.left = None
right_part = self.del_val(node.right, val) # 如果左侧递归到最后一个左结点,返回值还是空,就从左侧最后一层,开始向右递归
if right_part:
self.flag = True
node.right = None
return None # 如果遍历完二叉树,发现都没找到,说明要删除的值二叉树不存在
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
print("删除前:")
t.pre_oreder(t.root)
print()
del_res = t.del_val(t.root, 1)
# del_res = t.del_val(t.root, 16) # "要删除的值,二叉树中不存在"
# del_res = t.del_val(t.root, 0) # "删除根结点,二叉树置空"
if del_res == -1:
print("删除根结点,二叉树置空")
elif t.flag:
print("删除后:")
t.pre_oreder(t.root)
elif not t.flag:
print("要删除的值,二叉树中不存在")
'''
删除前:
0 1 3 7 8 4 9 2 5 6
删除后:
0 2 5 6
'''
'''
可以任意输入一个要删除的不存在二叉树的值,会返回"要删除的值,二叉树中不存在"
'''
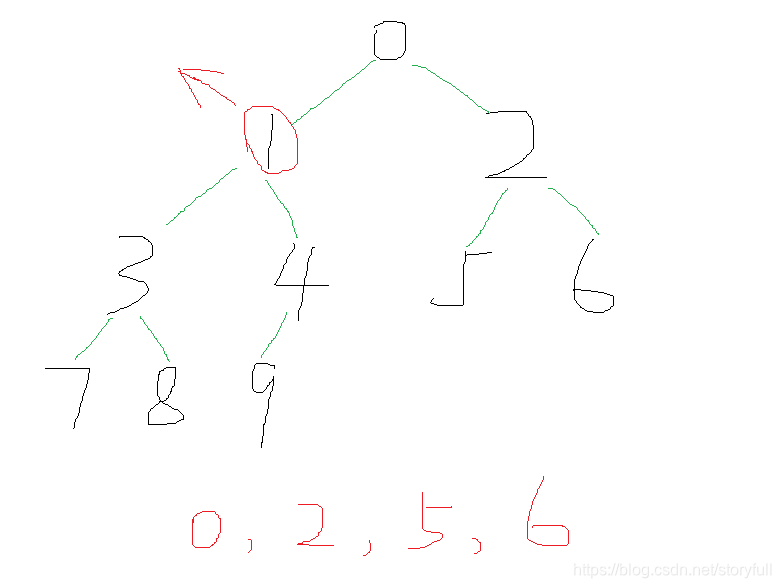
-
如果不删除二叉树的根结点(如果删除根结点,需要按照二叉搜索树的变换规则),这里规定不删除二叉树的第一个结点,那么可以这样实现:
(1)关键是 先获取 待删除节点值 val 的父节点,上面查找里已经写了获取父结点的方法,这里直接拿来用就可以了!具体操作过程如下:

class TreeNode(object):
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
def add(self, val): # 添加结点
node = TreeNode(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def pre_oreder(self, node): # 用前序遍历来测试 删除前和删除后的数据
if node is None:
return
stack = []
temp_node = node
while temp_node or stack:
while temp_node:
print(temp_node.val, end=" ")
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop(-1)
temp_node = node.right
def get_parent(self, val): # 二叉树查找父结点
if self.root.val == val: # 根结点没有父结点
return None
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left and temp_node.left.val == val:
return temp_node
if temp_node.right and temp_node.right.val == val:
return temp_node
if temp_node.left:
queue.append(temp_node.left)
if temp_node.right:
queue.append(temp_node.right)
return None
def del_val(self, val):
if self.root is None: # 如果根为空,直接返回
return False
parent = self.get_parent(val) # 获取到要删除节点值得父结点
if parent:
del_node = parent.left if parent.left.val == val else parent.right # 待删除节点
if del_node.left is None: # 左子树为空
if parent.left.val == val:
parent.left = del_node.right
else:
parent.right = del_node.right
del del_node
return True
elif del_node.right is None: # 右子树为空
if parent.left.val == val:
parent.left = del_node.left
else:
parent.right = del_node.left
del del_node
return True
else: # 左右子树都不为空
tmp_pre = del_node
tmp_next = del_node.right
if tmp_next.left is None:
# 替代
tmp_pre.right = tmp_next.right
tmp_next.left = del_node.left
tmp_next.right = del_node.right
else:
while tmp_next.left: # 让tmp指向右子树的最后一个叶子
tmp_pre = tmp_next
tmp_next = tmp_next.left
# 替代
tmp_pre.left = tmp_next.right
tmp_next.left = del_node.left
tmp_next.right = del_node.right
if parent.left.val == val:
parent.left = tmp_next
else:
parent.right = tmp_next
del del_node
return True
else:
return False
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
print("删除前:")
t.pre_oreder(t.root)
print()
print(t.del_val(4))
print("删除后:")
t.pre_oreder(t.root)
''' 输出结果:可以对照上面的图比较下
删除前:
0 1 3 7 8 4 9 2 5 6
True
删除后:
0 1 3 7 8 9 2 5 6
'''






















 2265
2265











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








