在n个球中，任意取出m个（不放回），求有多少种不同取法。（递归学习）

本文链接：https://blog.csdn.net/summer_lele/article/details/107202712

在n个球中，任意取出m个（不放回），求有多少种不同取法？

熟悉那么？

大家都应该首先想到

我们所学习过的

排列组合！

这题就是典型的组合问题（从不同元素中抽取部分元素的问题）

在这里插入图片描述

        组合（combination），数学的重要概念之一。从n个不同元素中每次取出m个不同元素（0≤m≤n），不管其顺序合成一组，称为从n个元素中不重复地选取m个元素的一个组合。所有这样的组合的总数称为组合数，这个组合数的计算公式为：

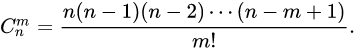
在这里插入图片描述

or
在这里插入图片描述

那么我们应该怎么用程序的形式表现出来呢？

这里小编使用

java语言和递归方法

向大家展示。


```java
public class CombinationCatchProblem {
  static int catchball(int n, int m) {

    if (n < m) {  
      return 0;
    }
    if (n == m) {
      return 1;
    }
    if (m == 0) {
      return 1;
    }
    return catchball(n - 1, m - 1) + catchball(n - 1, m);//分两种情况：1、从n中取出的球恰好是m中的；2、从n中取出的球不是m中的
  }

  public static void main(String[] args) {
    System.out.println(catchball(10, 3));
  }
}

在这里插入图片描述


主要思想就是：分两种情况进行递归求和：

                1、从n中取出的球恰好是m中的；

                2、从n中取出的球不是m中的


									如果对你有帮助就转发一下吧~谢谢