java 实现跳跃表

最新推荐文章于 2024-09-08 19:40:03 发布

MarthinMr

最新推荐文章于 2024-09-08 19:40:03 发布

阅读量3.8k

点赞数

分类专栏： Java 数据结构文章标签：跳跃表数据结构算法链表 java

本文链接：https://blog.csdn.net/sun_ru/article/details/51917273

版权

Java 数据结构专栏收录该内容

29 篇文章 0 订阅

订阅专栏

跳跃表是一种随机化的数据结构，效率接近二叉查找树，基于并联链表。本文介绍了跳跃表的原理和实现，包括如何通过抛硬币决定插入层数，以及如何保证查询效率为O(log n)。同时，文章提供了节点类和跳跃表类的简单描述，包括节点的四个方向和操作方法。

摘要由CSDN通过智能技术生成

跳跃链表是一种随机化数据结构，基于并联的链表，其效率可比拟于二叉查找树(对于大多数操作需要O(log n)平均时间)，并且对并发算法友好。

基本上，跳跃列表是对有序的链表增加上附加的前进链接，增加是以随机化的方式进行的，所以在列表中的查找可以快速的跳过部分列表(因此得名)。所有操作都以对数随机化的时间进行。

实现原理：

跳跃表的结构是：假如底层有10个节点，那么底层的上一层理论上就有5个节点，再上一层理论上就有2个或3个节点，再上一层理论上就有1个节点。所以从这里可以看出每一层的节点个数为其下一层的1/2个元素，以此类推。从这里我们可以看到，从插入时我们只要保证上一层的元素个数为下一层元素个数的1/2，我们的跳跃表就能成为理想的跳跃表。那么怎么才能保证我们插入时上层元素个数是下层元素个数的1/2呢，？很简单抛硬币就可以解决了，假设元素X要插入跳跃表，最底层是肯定要插入X的，那么次低层要不要插入呢，我们希望上层元素个数是下层的1/2，那么我们有1/2的概率要插入到次低层，这样就来抛硬币吧，正面就插入，反面就不插入，次次底层相对于次低层，我们还是有1/2的概率插入，那么就继续抛硬币吧，以此类推元，素X插入第n层的概率是(1/2)的n次。这样，我们能在跳跃表中插入一个元素了。

代码结构：

节点类：

String key 键值对跳跃表的操作都是根据键值进行的

Int value 实际值

Node up,down,left,right; 每个节点都有四个方向

String tou;

String wei; 每层链表的头和尾节点

跳跃表类：

Head 头节点

Tail 尾结点

H 层数

Size 元素个数

Random 随机数，用来确定需不需要增加层数即：掷硬币

findF () 按从小到大的顺序找到应该插入的位置插入排序法

Add () 添加节点函数，在最底层插入结点后，进行掷硬币来确定是否需要曾增加层数，直到掷硬币不能增加层数为止，增加层数的同事需要把增加之后的节点进行连接。

Find() 根据跳跃表进行查找并打印路线。查找从最上层开始然后找到被查找节点的前个节点小于被查找节点，然后被查找节点的后一个节点大于其被查找节点，则从被查找节点的前一个节点向下走down，然后继续向右查找，直到找到为止。

引用：http://www.java123.net/936905.html

跳跃表的引入

我们知道，普通单链表查询一个元素的时间复杂度为O(n)，即使该单链表是有序的，我们也不能通过2分的方式缩减时间复杂度。

如上图，我们要查询元素为55的结点，必须从头结点，循环遍历到最后一个节点，不算-INF(负无穷)一共查询8次。那么用什么办法能够用更少的次数访问55呢？最直观的，当然是新开辟一条捷径去访问55。

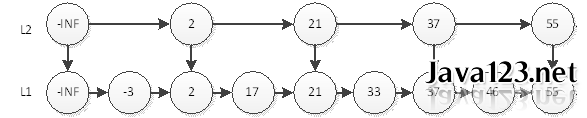
如上图，我们要查询元素为55的结点，只需要在L2层查找4次即可。在这个结构中，查询结点为46的元素将耗费最多的查询次数5次。即先在L2查询46，查询4次后找到元素55，因为链表是有序的，46一定在55的左边，所以L2层没有元素46。然后我们退回到元素37，到它的下一层即L1层继续搜索46。非常幸运，我们只需要再查询1次就能找到46。这样一共耗费5次查询。

那么，如何才能更快的搜寻55呢？有了上面的经验，我们就很容易想到，再开辟一条捷径。

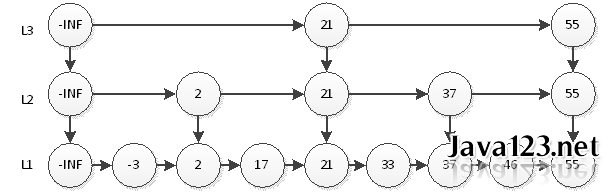
如上图，我们搜索55只需要2次查找即可。这个结构中，查询元素46仍然是最耗时的，需要查询5次。即首先在L3层查找2次，然后在L2层查找2次，最后在L1层查找1次，共5次。很显然，这种思想和2分非常相似，那么我们最后的结构图就应该如下图。

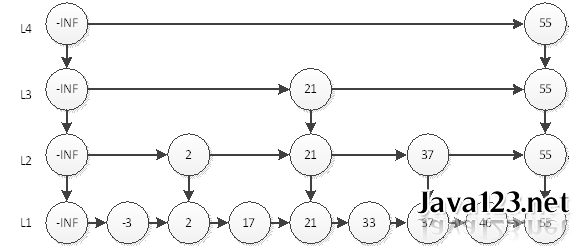
我们可以看到，最耗时的访问46需要6次查询。即L4访问55，L3访问21、55，L2访问37、55，L1访问46。我们直觉上认为，这样的结构会让查询有序链表的某个元素更快。那么究竟算法复杂度是多少呢？

如果有n个元素，因为是2分，所以层数就应该是log n层 (本文所有log都是以2为底)，再加上自身的1层。以上图为例，如果是4个元素，那么分层为L3和L4，再加上本身的L2，一共3层；如果是8个元素，那么就是3+1层。最耗时间的查询自然是访问所有层数，耗时logn+logn，即2logn。为什么是2倍的logn呢？我们以上图中的46为例，查询到46要访问所有的分层，每个分层都要访问2个元素，中间元素和最后一个元素。所以时间复杂度为O(logn)。

至此为止，我们引入了最理想的跳跃表，但是如果想要在上图中插入或者删除一个元素呢？比如我们要插入一个元素22、23、24……，自然在L1层，我们将这些元素插入在元素21后，那么L2层，L3层呢？我们是不是要考虑插入后怎样调整连接，才能维持这个理想的跳跃表结构。我们知道，平衡二叉树的调整是一件令人头痛的事情，左旋右旋左右旋……一般人还真记不住，而调整一个理想的跳跃表将是一个比调整平衡二叉树还复杂的操作。幸运的是，我们并不需要通过复杂的操作调整连接来维护这样完美的跳跃表。有一种基于概率统计的插入算法，也能得到时间复杂度为O(logn)的查询效率，这种跳跃表才是我们真正要实现的。

容易实现的跳跃表

容易实现的跳跃表，它允许简单的插入和删除元素，并提供O(logn)的查询时间复杂度，以下我们简称为跳跃表。

先讨论插入，我们先看理想的跳跃表结构，L2层的元素个数是L1层元素个数的1/2，L3层的元素个数是L2层的元素个数的1/2，以此类推。从这里，我们可以想到，只要在插入时尽量保证上一层的元素个数是下一层元素的1/2，我们的跳跃表就能成为理想的跳跃表。那么怎么样才能在插入时保证上一层元素个数是下一层元素个数的1/2呢？很简单，抛硬币就能解决了！假设元素X要插入跳跃表，很显然，L1层肯定要插入X。那么L2层要不要插入X呢？我们希望上层元素个数是下层元素个数的1/2，所以我们有1/2的概率希望X插入L2层，那么抛一下硬币吧，正面就插入，反面就不插入。那么L3到底要不要插入X呢？相对于L2层，我们还是希望1/2的概率插入，那么继续抛硬币吧！以此类推，元素X插入第n层的概率是(1/2)的n次。这样，我们能在跳跃表中插入一个元素了。

代码：

package 跳跃表;
import java.util.*;
public class SkipList {
	public Node head;	//头节点
	public Node tail;	//尾结点
	public int h;	//层数
	public int size;	//元素个数
	public Random rand;	//每次的随机数用来确定需不需要增加层数
	public SkipList(){
		Node p1 = new Node(Node.tou,0);
		Node p2 = new Node(Node.wei, 0);
		head=p1;
		tail=p2;
		head.setRight(tail);
		tail.setLeft(head);
		h=0;
		size=0;
		rand = new Random();
	}
	public boolean isEmpty(){
		if(size==0){
			return true;
		}
		return false;
	}
	//找到需要插入位置的前一个节点
	public Node findF(String k){
		Node temp;
		temp=head;
		while(true){
			while(temp.getRight().key!=Node.wei&&temp.getRight().key.compareTo(k)<=0){
				/*
				 * 当链表最底层不为空的时候，从当前层向尾部方向开始查找，直到查找temp.getRight的下一个值大于 当前k的值为止，此时temp小于或等于当前k的值
				 *  要插入的位置即为temp之后的位置了
				 */
				temp=temp.getRight();
			}
			if(temp.getDown()!=null){
				temp=temp.getDown();
			}else{
				break;
			}
			
		}
		return temp;	//找到节点并返回
		
	}
	public int add(String k, int v){
		Node temp, temp1;
		temp=findF(k);
		int i;	//当前层数
		if(k.equals(temp.getKey())){
			System.out.println("对象属性完全相同无法添加！");
			int a=temp.value;
			temp.value=v;
			return  a;
		}
		temp1=new Node(k,v);
		temp1.setLeft(temp);
		temp1.setRight(temp.getRight());
		temp.getRight().setLeft(temp1);
		temp.setRight(temp1);
		i=0;
		
		while(rand.nextDouble()<0.5){	//进行随机，是否需要 在上层添加
			if(i>=h){	//若当前层数超出了高度，则需要另建一层
				Node p1 ,p2 ;
				h=h+1;
				p1=new Node(Node.tou,0);
				p2=new Node(Node.wei,0);
				
				p1.setRight(p2);
				p1.setDown(head);
				
				p2.setLeft(p1);
				p2.setDown(tail);
				
				head.setUp(p1);
				tail.setUp(p2);
				
				head=p1;
				tail=p2;
			}
			while(temp.getUp() == null){
				temp=temp.getLeft();
			}
			temp=temp.getUp();
			Node node=new Node(k,v);
			node.setLeft(temp);
			node.setRight(temp.getRight());
			node.setDown(temp1);
			
			temp.getRight().setLeft(node);
			temp.setRight(node);
			temp1.setUp(node);
			
			temp1=node;
			i=i+1;	
			
		}
			
		size=size+1;
		return  0;
	}
	//节点查找
	public Node find(String k){
		Node temp=head;
		Node node;
		node=temp;
		System.out.println("查找路线");	//用于测试
		while(temp!=null){
			while(node.getRight().key!=Node.wei&&node.getRight().getKey().compareTo(k)<=0){//&&node.getRight().getValue()!=v
				node=node.getRight();
				System.out.print("--->"+node.getKey());
			}
			
			if(node.getDown()!=null){
				node=node.getDown();
				System.out.print("--->"+node.getKey());
			}else{
				if(node.key.equals(k)){//&&node.getRight().value==v
					//node.setValue(111111111);	//修改
					System.out.println("--->"+node.getKey());
					System.out.print("--->"+node.getValue());
					
					return node;													
				}
				return null;
			}
			
			
		}
		return null;
	}
	//节点删除
	public void delNode(String k){	//调用查找函数，删除最底层的某个节点，并把其节点的左右相连，和链表操作一样，只是其上方若有则都需要调整
		Node temp=find(k);
		while(temp!=null){
			temp.getLeft().setRight(temp.getRight());
			temp.getRight().setLeft(temp.getLeft());
			temp=temp.getUp();
		}
	}
	public void print(){
		Node node;
		Node node1=head;
		
		
		while(node1!=null){
			int k=0;
			node=node1;
			while(node!=null){
				System.out.print(node.getKey()+"\t");
				k++;
				node=node.getRight();
			}
			
			System.out.print("\t");
			System.out.print("("+k+")");
			//System.out.print(node.getKey());
			System.out.println();
			//node=node1.getDown();
			node1=node1.getDown();
			
		}
	}
	
}
class Node{
	public String key;
	public int value;
	public Node up, down,left , right;
	public static String tou=new String("--头--");
	public static String wei=new String("--尾--");
	public Node(String k, int v){
		this.key=k;
		this.value=v;
		up=down=left=right=null;
	}
	public void setUp(Node up){
		this.up=up;
	}
	public Node getUp(){
		return up;
	}
	public void setDown(Node down){
		this.down=down;
	}
	public Node getDown(){
		return down;
	}
	public void setLeft(Node left){
		this.left=left;
	}
	public Node getLeft(){
		return left;
	}
	public void setRight(Node right){
		this.right=right;
	}
	public Node getRight(){
		return right;
	}
	public void setKey(String k){
		this.key=k;
	}
	public String getKey(){
		return key;
	}
	public void setValue(int v){
		this.value=v;
	}
	public int getValue(){
		return value;
	}
	
}

package 跳跃表;

public class Test {
	public static void main(String[] args){
		SkipList s = new SkipList();
//		s.add("AAA", 122);
		int i=0;
		for(;i<30;i++){	//随机数字进行测试
			s.add(String.valueOf(i), i);
		}
		s.print();
		System.out.println("\n\n----------\n\n\n");				
		if(s.find("22")!=null){	//查找
			System.out.println("\nOK");
		}else{//找不到
			System.out.println("\nfalse");
			
		}
		s.delNode("0");	//删除
		s.print();
	}
}
测试结果：