8.4 贪心策略例题---区间选点问题

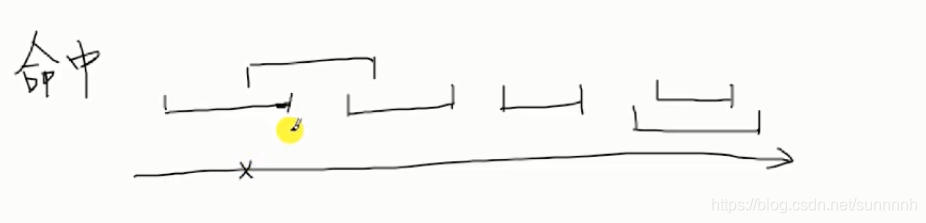
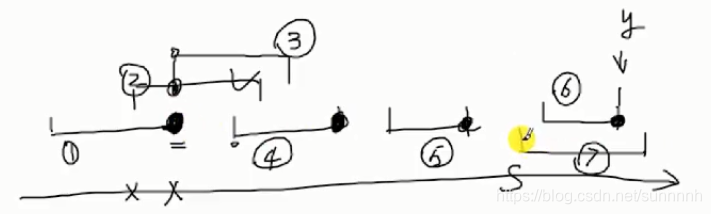
例题1：在区间内找尽可能少的点，能够命中所有区间

也是对开始和结束时间排序（结束时间从小到大排），每次选取结束时间点作为一个点，命中的区间数最大

如果选取一个区间的终点，命中了多个区间，接着再从未命中区间的终点开始选取点

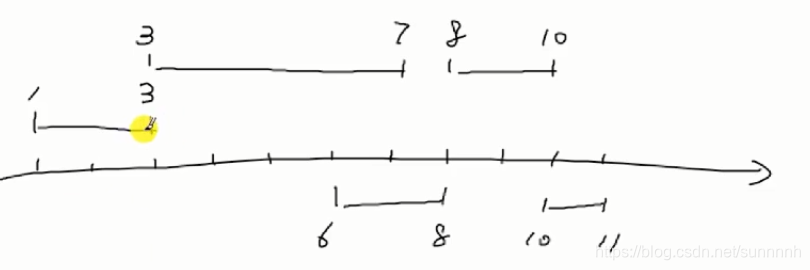
例题2（在上题基础上的提高）：要求每个区间有多个点

输入：

n（表示n个区间）

接下来n行输入 （每行三个数）

每个区间的开始时间 结束时间  含有点的个数

输出：

最少需要多少点

例如

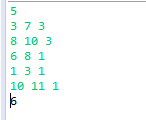
输入：

输出：

import java.util.Arrays;
import java.util.Scanner;

public class Main {
 /*
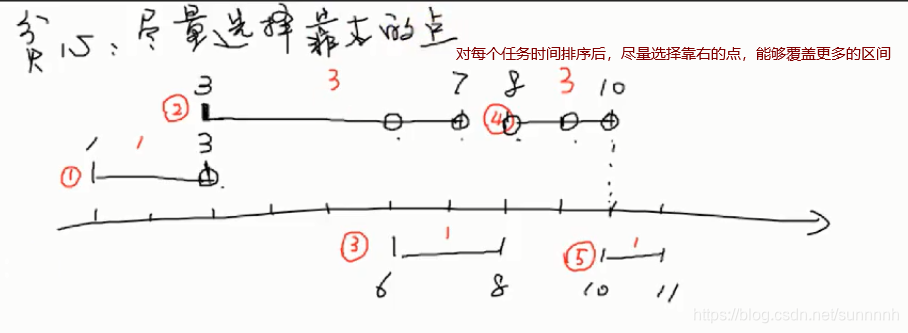
	 *思路：(1)首先将每个任务的开始时间、结束时间、需要包含的点封装在对象中，并按照结束时间递增排序（结束时间相同，按照开始时间递增排序）
	 *    (2)依次遍历每一个区间
	 *    	      查找该区间已存在的点
	 *          如果已存在的点==其需要的点，则继续遍历下一个区间
	 *          如果已存在的点<其需要的点，则从右向左为其分配点，并更新其所需的点，直到其所需的点为0
	 *关键：判断某个点是否已存在：建立一个数组axs作为数轴，其范围1~所有任务中最晚的结束时间，如果位置i已经设点，将axs[i]=1
	 *测试数据：
5
3 7 3
8 10 3
6 8 1
1 3 1
10 11 1
	
  */
	public static void main(String[] args) {
		//（1）输入相关数据
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[][] a = new int[n][3];
		for(int i=0;i<n;i++) {
			a[i][0] = sc.nextInt();//开始时间
			a[i][1] = sc.nextInt();//结束时间
			a[i][2] = sc.nextInt();//需要的点数
		}
		
		//（2）将每个区间开始、结束时间、需要的点数封装起来，并排序
		Task[] task = new Task[n];
		for(int i=0;i<n;i++) {
			task[i] = new Task(a[i][0],a[i][1],a[i][2]);
		}
		//排序
		Arrays.sort(task);
		
		//（3）设置一个数组axs作为数轴，记录被占用的点。1表示被占用
		int max = task[n-1].e;//最后一个任务的结束时间是数轴中最大的点
		int[] axs = new int[max+1];//下标0~max
		
		//(4)依次遍历每个任务，为其加点
		for(int i=0;i<n;i++) {
			int start=task[i].s;
			int end=task[i].e;
			int sum = getSumPoint(start,end,axs);//获取当前区间已存在的点数
			while(sum<task[i].c) {//点数不足，继续从右向左加点.注意：是while循环
				if(axs[end]==0) {//最右端没有加点
					axs[end]=1;
					end--;
					sum++;
				}else {
					end--;
				}
			}
		}
		System.out.println(getSumPoint(1, max, axs));
		
	}

//获取区间s~e中已存在的点数
private static int getSumPoint(int s, int e, int[] axs) {
	int cnt=0;
	for(int i=s;i<=e;i++) {
		cnt+=axs[i];
	}
	return cnt;
}
	
}
class Task implements Comparable<Task>{
	int s;//开始时间
	int e;//结束时间
	int c;//需要的点数
	public Task(int s, int e, int c) {
		super();
		this.s = s;
		this.e = e;
		this.c = c;
	}
	@Override
	public int compareTo(Task other) {
		int x = this.e-other.e;
		if(x==0) {//结束时间相等
			return this.s-other.s;
		}else {
			return x;
		}
		
	}
	
}