题目
给定一个源串和目标串,能够对源串进行如下操作:
1.在给定位置上插入一个字符
2.替换任意字符
3.删除任意字符
写一个程序,返回最小操作数,使得对源串进行这些操作后等于目标串,源串和目标串的长度都小于2000。
思路
如果有两个串 A = xabcdae 和 B = xfdfa,它们的第一个字符是相同的,只要计算A[2…7] = abcdae 和 B[2…5] = fdfa的距离就可以了。但是如果两个串的第一个字符不相同,那么可以进行如下的操作(lenA和lenB分别是字符串A和B的长度):
(1)删除A串的第一个字符,然后计算A[2…lenA]和B[1…lenB]的距离。
(2)删除B串的第一个字符,然后计算A[1…lenA]和B[2…lenB]的距离。
(3)修改A串的第一个字符为B串的第一个字符,然后计算A[2…lenA]和B[2…lenB]的距离。
(4)修改B串的第一个字符为A串的第一个字符,然后计算A[2…lenA]和B[2…lenB]的距离。
(5)增加B串的第一个字符到A串的第一个字符之前,然后计算A[1…lenA]和B[2…lenB]的距离。
(6)增加A串的第一个字符到B串的第一个字符之前,然后计算A[2…lenA]和B[1…lenB]的距离。
在这个题目中,我们并不在乎两个字符串变得相等之后的字符串是什么样的。所以,我们可以将上面的6个步骤简化为:
(1)一步操作之后,再将A[2…lenA] 和 B[1…lenB]变成相同的字符串。
(2)一步操作之后,再将A[1…lenA] 和 B[2…lenB]变成相同的字符串。
(3)一步操作之后,再将A[2…lenA] 和 B[2…lenB]变成相同的字符串。
这样,很快就可以完成一个递归程序:
代码
/*---------------------------------------------
* 日期:2015-02-16
* 作者:SJF0115
* 题目: 字符串编辑距离
* 来源:
* 博客:
-----------------------------------------------*/
#include <iostream>
using namespace std;
class Solution {
public:
int StrDistance(string A,string B){
int sizeA = A.size();
int sizeB = B.size();
return StrDistance(A,0,sizeA-1,B,0,sizeB-1);
}
private:
int StrDistance(string A,int startA,int endA,string B,int startB,int endB){
if(startA > endA){
// 字符串A和B到末尾
if(startB > endB){
return 0;
}//if
// 字符串A到末尾 B未到
else{
return endB - startB + 1;
}
}//if
// 字符串B到末尾 A未到
if(startB > endB && startA <= endA){
return endA - startA + 1;
}//if
// 字符串A和B均未到末尾
if(A[startA] == B[startB]){
return StrDistance(A,startA+1,endA,B,startB+1,endB);
}//if
else{
int len1 = StrDistance(A,startA+1,endA,B,startB,endB);
int len2 = StrDistance(A,startA,endA,B,startB+1,endB);
int len3 = StrDistance(A,startA+1,endA,B,startB+1,endB);
return min(min(len1,len2),len3)+1;
}//else
}
};
int main() {
Solution solution;
string str1("xabcdae");
string str2("xfdfa");
cout<<solution.StrDistance(str1,str2)<<endl;
}
上面的思路还可以进行优化。在递归的过程中,有些数据被重复计算了。比如,如果我们开始调用StrDistance(A,1,3,B,1,3)
下图是部分展开的递归调用:
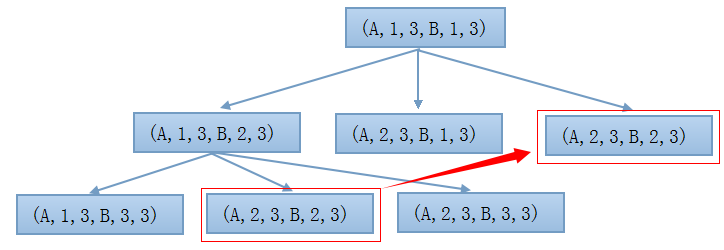
可以看到,圈中的两个子问题被重复计算了。为了避免这种不必要的重复计算,可以把子问题计算后的解储存起来。
思路二
编辑距离是动态规划里面的经典题目。 Edit[i][j]为word1[0..i-1]和word2[0..j-1]的最小编辑数。
状态转移方程:
代码二:
/*--------------------------------------------
* 日期:2014-03-01
* 作者:SJF0115
* 题目: 72.Edit Distance
* 网址:https://oj.leetcode.com/problems/edit-distance/
* 结果:AC
* 来源:LeetCode
* 博客:
------------------------------------------------*/
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size();
int n = word2.size();
// Edit[i][j]为word1[0..i-1]和word2[0..j-1]的最小编辑数
int Edit[m+1][n+1];
// 初始化
for(int i = 0;i <= m;++i){
Edit[i][0] = i;
}//for
for(int i = 0;i <= n;++i){
Edit[0][i] = i;
}//for
for(int i = 1;i <= m;++i){
for(int j = 1;j <= n;++j){
// 当前字符相同
if(word1[i-1] == word2[j-1]){
Edit[i][j] = Edit[i-1][j-1];
}//if
else{
Edit[i][j] = 1 + min(Edit[i-1][j-1],min(Edit[i-1][j],Edit[i][j-1]));
}//else
}//for
}//for
return Edit[m][n];
}
};
int main(){
Solution solution;
string str1("ab");
string str2("bc");
cout<<solution.minDistance(str1,str2)<<endl;
return 0;
}








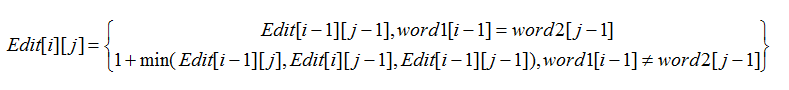

















 2315
2315

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










