【每日一题】LeetCode - 动态规划题目(2)

1. 70. 爬楼梯 (https://leetcode-cn.com/problems/climbing-stairs/)

• 本题是很经典的动态入门的规划题目，可以从递归问题入手，分析重叠子问题，再优化递归解法为带备忘录算法的递归解法，再进一步将递归自顶向下的解题思路转化为自底向上，最终实现动态规划的算法。

  class Solution {
      public int climbStairs(int n) {
          if (n <= 3) return n; 
          int prev = 1;
          int curr = 2;
          for(int i = 3; i <= n; ++i) {
              int temp = curr;
              curr+=prev;
              prev = temp;
          }
          return curr;
      }
  }
  

2. 198. 打家劫舍 (https://leetcode-cn.com/problems/house-robber/)

• 本题同样可以画一个递归树思考：
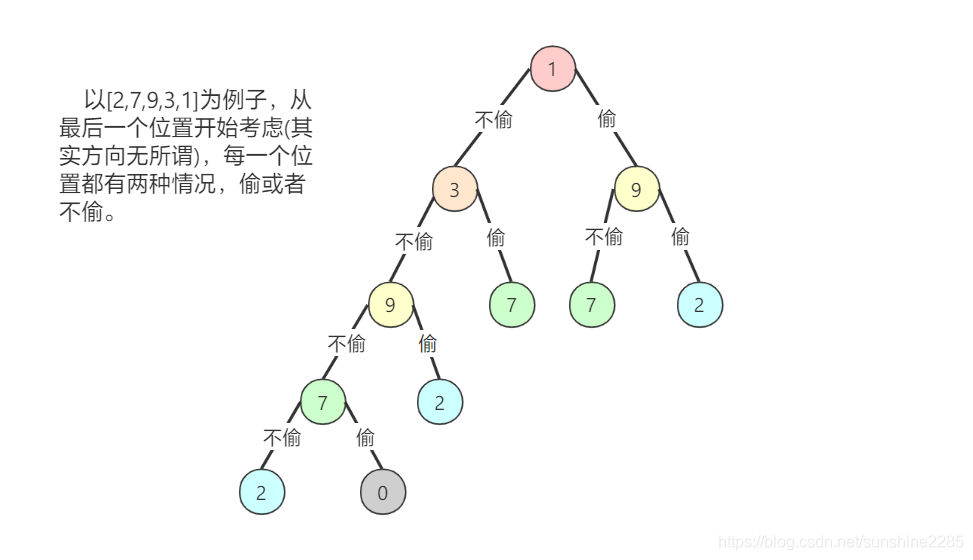
• 从上述的递归树可以看出，这个问题的解其实可以看做是找出改决策树权值最大的一条路径。仔细观察，在递归过程中存在很多重复计算，如以9、7、2为根节点的子树，消除这些重复子问题的冗余计算便是解题的关键，可以使用备忘录算法。
• 而动态规划的思想可以从自底向上研究递归树发现，每一个根节点的最大值可通过左右孩子获得，即
• $根节点的最大值=Max(左孩子的最大值，右孩子的最大值+根节点值)$。
• 对 $dp[i]$ 的解释：$dp[i]$ 表示以第 $i$ 个为终点，可偷到的最大值。
• 用动态规划的术语即：$dp[i]=Max(dp[i-1],dp[i-2]+nums[i])$【状态转移方程】
• 对状态转移方程的解释：第 $i$ 个屋子的最大价值为 第$i$个屋子的价值与第$i-2$个屋子最大价值的和 与 第$i-1$ 个屋子的最大价值 两者中的最大值。

  class Solution {
      public int rob(int[] nums) {
          if(nums.length == 0) return 0;
          int last = nums[0];
          int llast = 0;
          for(int i = 1; i < nums.length; ++i) {
              int temp = last;
              last = Math.max(last, llast + nums[i]);
              llast = temp;
          }
          return last;
      }
  }
  

3. 413. 等差数列划分 (https://leetcode-cn.com/problems/arithmetic-slices/)

• 这道题确实一开始确实没有想出来动态规划的解法，是看了题解才知道的。

• 先看一种比较直观的解法：从系列中找最长的等差数列，每找到一个就统计所有等差子列个数和并累加到总数中，直到找完所有等差数列。

• 这种算法的效果还是比较不错了，主函数的时间复杂度是O(n*O(f))，其中 f 为计算一个长度为n的等差数列的所有子数列的个数(这里的f，我看到题解有数学公式 $n\ast (n+1)/2$，n为等差数列长度)；

  class Solution {
      public int numberOfArithmeticSlices(int[] nums) {
          if(nums == null || nums.length < 3) {
              return 0;
          }
  
          int count = 0;
          int start = 0;
          int end = 1;
          int gap = nums[1] - nums[0];
      
          for(int i = 2; i < nums.length; ++i) {
              if(nums[i] - nums[i-1] == gap) {
                  ++end;
              } else {
                 if (end - start >= 2) {
                      count += statistic(start, end);
                  }
                  start = i - 1;
                  end = i;
                  gap = nums[i] - nums[i - 1];
              }
          }
          if(end - start >= 2) {
              count += statistic(start, end);
          }
          return count;
      }
      private int statistic(int s, int e) {
          int len = e - s + 1;
          int count = 1;
          for(int i = 3; i < len; ++i) {
             for (int j = s; j + i - 1 <= e; ++j) {
                  ++count;
              }
          }
          return count;
      }
  }
  

• 动态规划的解法

• $dp[i]$ 表示以第$i$个元素为结尾的等差数列的个数

• 当第$i$个元素和之前元素构成等差数列($nums[i]-nums[i-1]==nums[i-1]-nums[i-2]$)，则 $dp[i]=dp[i-1]+1$，否则$dp[i]=0$;【状态转移方程】

• 对状态转移方程的解释：如果不与之前的元素构成等差数列，则$dp[i]=0$，这个很好理解。难点在于构成等差数列时，首先我们需要明确$dp[i]$的含义，$dp[i]$表示以第$i$个元素结尾的等差数列的个数，那$dp[i-1]$表示以第$i-1$个元素为结束的等差数列的个数，所有以第$i-1$个元素为结束的等差数列在加上第$i$个元素时都会构成新的等差数列，而+1的原因是第$i$ 个元素还会与第$i-1$,第$i-2$个元素构成新的等差数列，所以$dp[i]=dp[i-1]+1$;

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        if(nums == null || nums.length < 3) {
            return 0;
        }
        int dp = 0;
        int sum = 0;
        for(int i = 2; i < nums.length; ++i) {
            if(nums[i] - nums[i-1] == nums[i-1] - nums[i-2]) {
                dp += 1;
                sum += dp;
            }else {
                dp = 0;
            }
        }
        return sum;
    }
}