【Graph Embedding】: node2vec算法

DivinerShi

于 2019-03-27 23:33:42 发布

阅读量3.4k

点赞数

分类专栏：深度学习推荐系统 graph embedding

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/sxf1061926959/article/details/88831720

版权

深度学习同时被 3 个专栏收录

33 篇文章

订阅专栏

18 篇文章

订阅专栏

graph embedding

5 篇文章

订阅专栏

论文“node2vec: Scalable Feature Learning for Networks”发表在kdd2016，文章提出了一个新的graph embedding

论文地址：https://www.kdd.org/kdd2016/papers/files/rfp0218-groverA.pdf

作者提供的代码地址：http://snap.stanford.edu/node2vec/

微信将node2vec用于广告lookalike的应用：微信的广告投放策略

算法“node2vec”。算法定义了一个图中节点邻域的灵活概念，并设计了一个带偏置的随机游走过程，用于有效的探索不同的邻域。作者认为在探索邻域时的灵活性是学习出更丰富节点表示的关键。

其实node2vec算法算是deepwalk的一个扩展，如果将节点采样问题看成一种局部搜索的形式的话，那么deepwalk中的随机游走，有点类似于邻域的深度优先搜索。而node2vec通过引入两个参数来控制随机游走，做到来相当于深度优先搜索和广度优先搜索的结合，可以自由控制邻域探索的方式，再针对提取的邻域利用SGD进行优化。。

本文提出了一个用于大尺度网络特征表示的半监督算法node2vec。利用二阶的随机游走策略来采样节点的邻域节点。

特征学习框架（Feature learning framework）

将特征学习问题定义为最大似然优化问题，定义网络G(V,E)，令 $f: V\rightarrow R^d$ 是我们要学习的函数f，表示节点到特征表示的一个映射函数。d是embedding的维度。f就是我们学习出来的embedding矩阵。对于每个节点 $u\in V$ ,定义 $N_S(u)\subset V$ 作为节点u通过邻域采样策略S生成的邻域节点。

优化目标：最大化在节点u的条件下，出现其邻域节点的对数概率，节点u用其由函数f生成的embedding向量表示，所以优化目标为：

为了简化优化问题，做了两个标准假设：

1.条件独立。假设节点u的邻域节点之间出现的概率相互独立，那么优化目标就可以变成：

2.特征空间对称性。即节点与节点之间是对称，所有的节点都在同一个空间下面。既然在同一个特征空间下面，那么我们可以把节点与其邻域节点的条件似然概率定义成softmax形式，如：

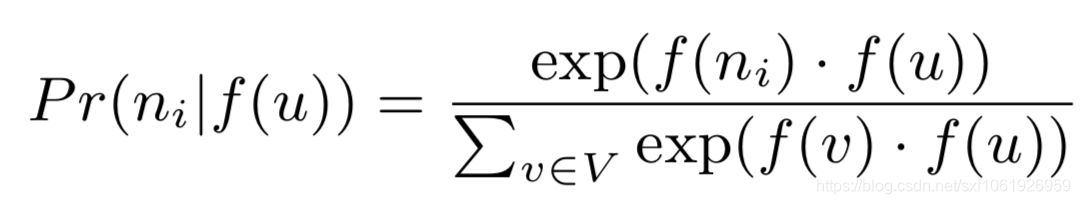
有了写两个假设，再把这两个公式带回原来的优化目标中，就能得到新的目标函数：

这里的 $Z_u=\sum_{v\in V}exp(f(u)\cdot f(v))$ 是归一化因子，这里就可以用上神经网络里面针对softmax的常用套路了，做负采样。

然后根据这个目标函数，直接利用skip-gram来学习embedding向量。其实这里和deepwalk的后半部是一样的，关键是怎么从graph中采样session出来给skip-gram训练。

采样策略

为了比较不同的抽样策略S，限制节点的邻域Ns为k个节点，然后为节点u采样多个集合。常用的邻域节点采样方法：

广度优先采样（BFS）：邻域节点的采样限制为和目标节点直接链接的节点。

深度优先采样（DFS）:邻域节点的采样按从源节点距离越来越远的顺序进行采样。

nodel2vec

文章设计了一个灵活的采样策略用于平衡BFS和DFS，即利用带偏置的随机游走策略来，该方式可以BFS和DFS的方式探索邻近区域。

随机游走（Random Walks）

先给出定义：给定一个源节点u，确定好随机游走的长度为l。用 $c_i$ 表示随机游走中的第i个节点，以 $c_0=u$ 开始，那么节点 $c_i$ 生成方式为：

其中 $\pi_{vx}$ 是节点v和节点x之间的未归一化的转移概率，Z是归一化因子。

搜索偏置

最简单的随机游走方法就是让 $\pi_{vx}=w_{vx}$ ,就是按边的权重分配等价的概率来选择下一个节点。但是这样就没发做邻域探索。所以作者提出了一个二阶的随机游走策略，利用两个参数p和q来控制游走。

如上图，假设现在经过随机游走，节点从t经过边(t,v)到来v，那么当前节点为v，游走策略需要确定下一个节点走哪里，这里设置未归一化转移概率为 $\pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx}$ ,其中

这里的 $d_{tx}$ 指的是节点t和节点x的最短路径距离，且 $d_{tx}$ 的范围是{0,1,2}中的一个，因此这两个用于知道游走的参数是十分必要的。

返回参数p(Return parameter p).返回参数p，参数p是控制下一个节点是否选择上一节点的概率，所以该参数的需要设置一个较大的值，确保我们小概率的采样一个已经访问过的节点，除非下一个节点没有其他邻域节点了。

内外参数q(In-out parameter q).参数q控制下一个游走的节点是靠近原来的节点还是远离原来的节点。如果q>1,那么随机游走偏向于靠近原始节点t，q<1则相反。

随机游走的优势。随机游走在空间和时间上都是比较有效的

算法的整个流程

这里预先计算了转移概率，并用alias采样算法可以在O(1)时间内完成采样。

完

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。