AES是一种对称加密算法,它的相关概念在此不赘述。
GCM ( Galois/Counter Mode) 指的是该对称加密采用Counter模式,并带有GMAC消息认证码。
在详细介绍AES-GCM之前,我们先了解一些相关概念。
下文中出现的符号:
| Ek | 使用秘钥k对输入做对称加密运算 |
| XOR | 异或运算 |
| Mh | 将输入与秘钥h在有限域GF(2^128)上做乘法 |
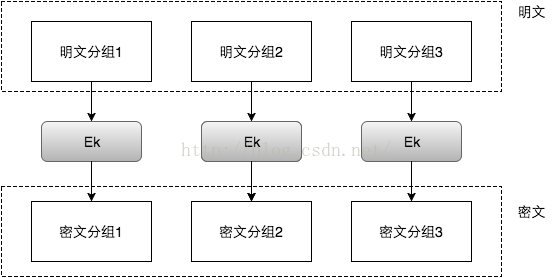
ECB( Electronic Mode 电子密码本模式)
由上图可以看出,明文中重复的排列会反映在密文中。
并且,当密文被篡改时,解密后对应的明文分组也会出错,且解密者察觉不到密文被篡改了。也就是说,ECB不能提供对密文的完整性校验。
因此,在任何情况下都不推荐使用ECB模式。
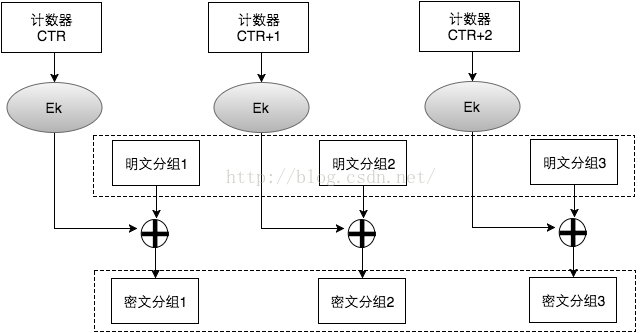
CTR ( CounTeR 计数器模式)
在计数器模式下,我们不再对密文进行加密,而是对一个逐次累加的计数器进行加密,用加密后的比特序列与明文分组进行 XOR得到密文。过程如下图:
计数器模式下,每次与明文分组进行XOR的比特序列是不同的,因此,计数器模式解决了ECB模式中,相同的明文会得到相同的密文的问题。CBC,CFB,OFB模式都能解决这个问题,但CTR的另两个优点是:1)支持加解密并行计算,可事先进行加解密准备;2)错误密文中的对应比特只会影响明文中的对应比特等优点。
但CTR仍然不能提供密文消息完整性校验的功能。
有的人可能会想到,如果将密文的hash值随密文一起发送,密文接收者对收到的密文计算hash值,与收到的hash值进行比对,这样是否就能校验消息的完整性呢?
再仔细想想,就能发现这其中的漏洞。当篡改者截获原始的密文消息时,先篡改密文,而后计算篡改后的密文hash, 替换掉原始消息中的密文hash。这样,消息接收者仍然没有办法发现对源密文的篡改。可见,使用单向散列函数计算hash值仍然不能解决消息完整性校验的问题。
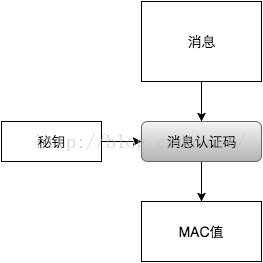
MAC ( Message Authentication Code, 消息验证码)
想要校验消息的完整性,必须引入另一个概念:消息验证码。消息验证码是一种与秘钥相关的单项散列函数。
如果生成密文的加密模式是CTR,或者是其他有初始IV的加密模式,别忘了将初始的计时器或初始向量的值作为附加消息与密文一起计算MAC。
GMAC ( Galois message authentication code mode, 伽罗瓦消息验证码 )
对应到上图中的消息认证码,GMAC就是利用伽罗华域(Galois Field,GF,有限域)乘法运算来计算消息的MAC值。假设秘钥长度为128bits, 当密文大于128bits时,需要将密文按128bits进行分组。应用流程如下图: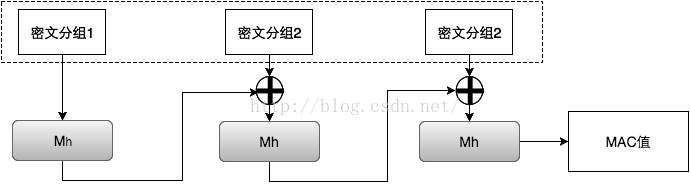
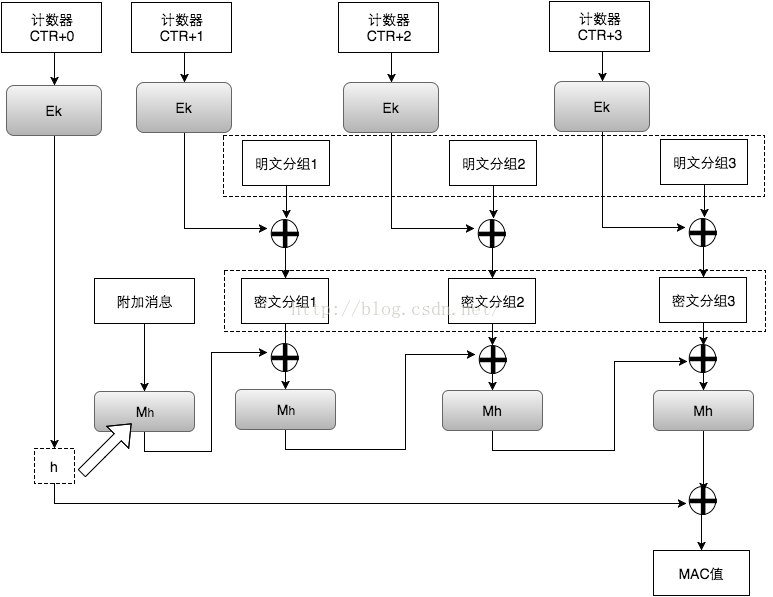
GCM( Galois/Counter Mode )
GCM中的G就是指GMAC,C就是指CTR。GCM可以提供对消息的加密和完整性校验,另外,它还可以提供附加消息的完整性校验。在实际应用场景中,有些信息是我们不需要保密,但信息的接收者需要确认它的真实性的,例如源IP,源端口,目的IP,IV,等等。因此,我们可以将这一部分作为附加消息加入到MAC值的计算当中。下图的Ek表示用对称秘钥k对输入做AES运算。最后,密文接收者会收到密文、IV(计数器CTR的初始值)、MAC值。





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








