5.2 线性模型：边界值问题-CSDN博客

本文探讨了物理系统中的线性微分方程，特别是梁的挠曲问题，通过边界条件解析了四阶微分方程，并介绍了特征值和特征函数的概念，以示例说明如何求解边界值问题，涉及欧拉载荷和旋转绳子模型的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

来源：小温Learning
本文约3200字，建议阅读9分钟
物理系统的数学描述通常要求我们解决一个线性微分方程，同时满足边界条件。

线性模型：边界值问题

引言：前面的部分讨论了具有二阶数学模型和初始条件的系统，即在未知函数及其一阶导数在单个点上指定的边界条件。但是，物理系统的数学描述通常要求我们解决一个线性微分方程，同时满足边界条件，即在未知函数上或其导数之一上，甚至是在未知函数和其导数之一的线性组合上，在两个（或更多）不同的点上指定的条件。

梁的挠曲：许多结构是通过使用梁或横梁构建的，在其自身重量或外部力的影响下，这些梁会发生挠曲或变形。正如我们将要看到的，这种挠曲由一个相对简单的线性四阶微分方程所控制。

首先，让我们假设一根长度为的梁是均匀的，并且在其长度上具有均匀的横截面。在梁上没有任何载荷（包括自身重量）的情况下，连接所有横截面质心的曲线是一条被称为对称轴的直线。参见图5.2.1(a)。如果在包含对称轴的垂直平面上对梁施加载荷，则梁会发生变形，如图5.2.1(b)所示，连接所有横截面质心的曲线称为挠曲曲线或弹性曲线。挠曲曲线近似表示了梁的形状。现在假设轴与对称轴重合，并且从该轴测量的挠度，如果向下为正。在弹性理论中，证明了梁上一点处的弯矩与单位长度载荷之间的关系由方程

此外，弯矩与弹性曲线的曲率成正比，即：

其中和是常数；是梁材料的杨氏模量，是梁的截面惯性矩（关于一个被称为中性轴的轴线）。乘积被称为梁的弯曲刚度。

现在，根据微积分，曲率由给出。当挠度很小时，斜率，因此。如果我们令，方程（2）变为。对此最后一个表达式进行二阶导数，得到：

将（1）中给出的结果用于替换（3）中的，我们可以看到挠度满足四阶微分方程：

与方程（4）相关的边界条件取决于梁的两端如何支撑。悬臂梁在一端嵌入或固定，另一端自由。跳水板、伸展的手臂、飞机机翼和阳台都是这种梁的常见例子，但即使是树木、旗杆、摩天大楼和乔治·华盛顿纪念碑也可以作为悬臂梁，因为它们在一端嵌入，并受到风力的弯曲力的影响。对于悬臂梁，挠度必须满足以下两个条件：

，因为没有挠度，
，因为挠度曲线在该点切线与轴平行（换句话说，挠度曲线在该点的斜率为零）。

在处，自由端的条件为：

，因为弯矩为零，
，因为剪力为零。

函数被称为剪力。如果梁的一端是简支或铰接（也称为铰链支承和支点支承），那么在该端点必须满足和。表5.2.1总结了与（4）相关的边界条件。见图5.2.2。

示例1：嵌入梁

一根长度为的梁在两端嵌入。如果一个恒定的载荷均匀分布在其长度上，即，求梁的挠度。

解：从（4）我们可以看出，挠度满足

因为梁在左端和右端都被嵌入，所以在这些点上没有垂直挠度，挠度线是水平的。因此边界条件是

我们可以以通常的方式解非齐次微分方程（通过观察到是辅助方程的四重根来找到，然后通过待定系数法找到一个特解），或者我们可以连续四次积分方程来求解。无论哪种方式，我们都可以找到方程的通解为

现在条件和依次给出和，而剩下的条件和应用于，得到联立方程组

解决这个系统得到和。因此挠度为

或者。通过选择和，我们得到图5.2.3中的挠度曲线。

特征值和特征函数

许多应用问题要求我们解决一个包含参数的线性微分方程的两点边界值问题（BVP）。我们寻找使得边界值问题具有非平凡解（即非零解）的的值。

示例2：BVP的非平凡解

解决边界值问题：

解决方案: 我们将考虑三种情况：和。

情况一：对于，的解为。将条件和应用于这个解，依次得到和。因此，对于，边界值问题的唯一解是平凡解。

情况二：对于，方便起见，我们写作，其中表示一个正数。利用这个记法，辅助方程的根为和。由于我们工作的区间是有限的，我们选择将的一般解写作。现在是

因此意味着。因此 sinh 。第二个条件要求。对于，sinh ；因此，我们被迫选择。再次，BVP的唯一解是平凡解。

情况三：对于，我们写作，其中是一个正数。由于辅助方程有复数根和，的一般解为。与前面一样，得到，因此。现在最后一个条件，或者

通过选择来满足。但这意味着。如果我们要求，那么只要，就满足条件，其中是的整数倍。

因此，对于任意实非零数，是问题的解，其中是正整数。由于微分方程是齐次的，任何解的常数倍也是解，因此我们可以选择。换句话说，对于序列中的每个数：

序列中对应的函数：

分别是问题的非平凡解。

对于，边界值问题在示例2中具有非平凡解的数被称为特征值。依赖于这些值的非平凡解或简单地被称为特征函数。图5.2.4显示了的特征函数的图形。请注意，每个图形通过点和。

示例3 重新审视示例2

根据示例2和前面的讨论，边界值问题：

只有平凡解，因为5不是特征值。

在18世纪，莱昂哈德·欧拉是最早研究特征值问题的数学家之一，他分析了一根细弹性柱在受到压缩轴向力时的屈曲现象。

考虑一根长而细的垂直柱，具有均匀的横截面和长度。当施加一个恒定的垂直压缩力或载荷到柱顶时，设表示柱的挠度，如图5.2.5所示。通过比较柱上任意点处的弯矩，我们得到

或者

其中是杨氏模量，是横截面关于通过其质心的垂直线的惯性矩。

示例4 欧拉载荷

如果柱在两端简支或铰支，求一根细长均质垂直柱在受到恒定轴向载荷时的挠度。

解: 这个问题的边界值问题是：

首先注意到是这个问题的一个完全合理的解。这个解有一个简单直观的解释：如果载荷不够大，就不会有挠度。那么问题是：的哪些值会使柱发生弯曲？用数学术语来说：给定的边界值问题存在非平凡解的的取值是多少？通过写成，我们可以看到：

与示例2中的问题完全相同。从讨论的第III种情况中，我们可以看到挠度为，对应于特征值。从物理上讲，这意味着只有当压缩力是值之一时，柱才会发生屈曲或挠曲。这些不同的力被称为临界载荷。对应于最小临界载荷的挠度，称为欧拉载荷，为，也称为第一屈曲模态。

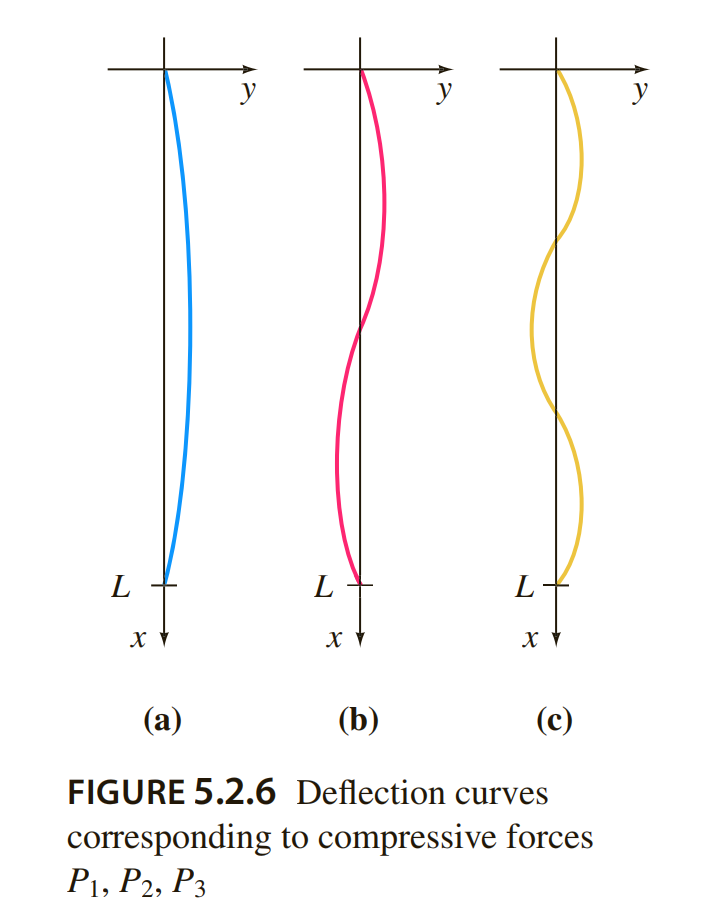
示例4中对应于和的挠曲曲线如图5.2.6所示。请注意，如果原始柱在处受到某种物理约束，则最小的临界载荷将为，挠曲曲线将如图5.2.6(b)所示。如果在柱子上放置了约束，在和处，则柱子直到施加临界载荷之前不会发生屈曲，挠曲曲线将如图5.2.6(c)所示。

旋转的绳子

这个简单的线性二阶微分方程：

一次又一次地出现作为一个数学模型。在5.1节中，我们以形式和看到了(6)，分别作为弹簧/质量系统的简谐运动和串联电路的简谐响应的模型。当将(5)中薄柱的挠曲模型写为时，很明显它与(6)是相同的。我们在本节中再次遇到基本方程(6)：作为定义旋转绳子的挠曲曲线或形状的模型。物理情况类似于两个人手持跳绳并以同步的方式旋转它。请参见图5.2.7(a)和5.2.7(b)。