狄拉克 δ 函数

来源：小温Learning
本文约1000字，建议阅读5分钟
我们将介绍一种与你之前学过的函数非常不同的函数。

狄拉克δ函数

引言 根据定理7.1.3的直接推论， 不能是定义在上分段连续且指数阶的函数的拉普拉斯变换。在接下来的讨论中，我们将介绍一种与你之前学过的函数非常不同的函数。我们将看到确实存在一个函数，或者更准确地说，一个广义函数，其拉普拉斯变换为。

单位脉冲 机械系统经常受到一个仅在很短时间内作用的大幅度外力（或电路中的电动势）。例如，振动的飞机机翼可能被雷击，弹簧上的质量可能被球锤猛击，当某种球类（棒球、高尔夫球、网球）被球棒、高尔夫球杆或网球拍猛击时，球可能会飞起。分段定义的函数的图像

，如图(a)所示，可以作为这种力的模型。对于较小的值，基本上是一个幅度很大的常数函数，仅在附近的一个非常短的时间内处于"开启"状态。当时，的行为如图(b)所示。函数被称为单位脉冲，因为它具有积分性质。

狄拉克δ函数 在实际应用中，使用另一种类型的单位冲激更为方便，即近似表示为  的“函数”，并通过极限定义如下：

后者并不是一个真正的函数，它可以通过以下两个特性来描述：(i)  和 (ii) .

单位脉冲  被称为狄拉克δ函数。可以通过形式上的假设

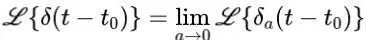
来获得狄拉克δ函数的拉普拉斯变换。

定理 7.5.1 狄拉克δ函数的变换

对于，

证明: 首先，我们可以将表示为单位阶跃函数的形式：

由于线性性，最后一个表达式的拉普拉斯变换为

在时具有不定形式，我们应用L'Hôpital法则：

现在当时，

最后一个结果强调了不是我们一直在考虑的通常类型的函数，因为根据定理7.1.3，我们期望，当时。

例1 两个初值问题

解，满足

(a) 

(b) 

这两个初值问题可以作为描述在阻尼可忽略的介质中运动的弹簧上的质量的运动的模型。在时，质量受到了一个尖锐的打击。在(a)中，质量从静止状态下降1个单位到平衡位置下方。在(b)中，质量处于平衡位置的静止状态。

解:(a) 微分方程的拉普拉斯变换为

我们得到

由于，上述解可以写成

从图中我们可以看到，质点在之前表现出简谐运动。单位冲激的影响是使振动的幅度增加到，对于。

(b) 在这种情况下，方程的变换简化为 因此

从图中可以看出，根据初始条件，质点在之前没有运动。