稀疏阶乘问题
题目概述
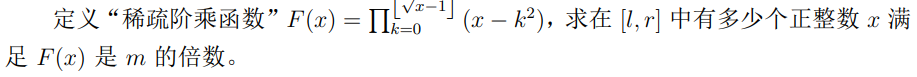
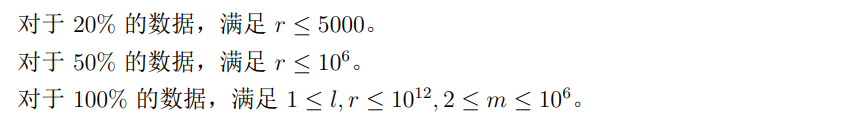
题解
我们发现
F
(
x
)
F(x)
F(x)是
m
m
m倍数是可以看作
F
(
x
)
%
m
=
0
F(x)\%m=0
F(x)%m=0的,也就是说
∏
(
x
−
k
2
)
\prod(x-k^2)
∏(x−k2)中包含了
m
m
m的所有质因子。
对每个质因子单独考虑。
如果
m
=
∏
i
=
1
k
p
i
m=\prod_{i=1}^k p_i
m=∏i=1kpi,我们的
F
(
x
)
=
0
F(x)=0
F(x)=0就相当于
∀
i
∈
[
1
,
k
]
,
∃
j
2
<
x
,
x
≡
j
2
(
m
o
d
p
i
)
\forall i\in[1,k],\exist j^2< x,x\equiv j^2\pmod{p_i}
∀i∈[1,k],∃j2<x,x≡j2(modpi)。
一种简单的思路是我们记录下来
m
n
i
,
j
mn_{i,j}
mni,j表示取模
p
i
p_i
pi余
j
j
j的最小完全平方数。
显然有
[
F
(
x
)
%
m
=
0
]
=
⋀
i
=
1
k
[
x
>
m
n
i
,
x
%
p
i
]
[F(x)\%m =0]=\bigwedge_{i=1}^k[x>mn_{i,x\%p_i}]
[F(x)%m=0]=⋀i=1k[x>mni,x%pi]。
但如果
m
=
∏
i
=
1
k
p
i
k
i
m=\prod_{i=1}^k p_i^{k_i}
m=∏i=1kpiki呢?这样许多
k
2
%
p
=
a
k^2\% p=a
k2%p=a的完全平方数贡献在一起可以抵一个
k
2
%
p
k
=
a
+
p
b
k^2\%p^k=a+pb
k2%pk=a+pb的效果。
诶,可以发现,我们只需要不超过
k
i
k_i
ki个这样的数就行了。
我们不妨暴力枚举
c
p
i
+
r
,
c
∈
[
1
,
k
i
]
cp_i+r,c\in[1,k_i]
cpi+r,c∈[1,ki],把它们贡献到所有满足
j
%
p
i
=
r
2
%
p
i
j\%p_i=r^2\%p_i
j%pi=r2%pi的
m
n
i
,
j
mn_{i,j}
mni,j上,记录每一个至少要撑到哪一个
c
p
i
+
r
cp_i+r
cpi+r,也就是找到最小的
l
i
m
lim
lim使得
∏
l
=
0
l
i
m
(
j
−
l
p
i
−
r
)
≡
0
(
m
o
d
p
i
k
i
)
\prod_{l=0}^{lim}(j-lp_i-r)\equiv 0\pmod{p_i^{k_i}}
∏l=0lim(j−lpi−r)≡0(modpiki),反正有
l
i
m
<
k
i
⩽
log
m
lim<k_i\leqslant \log m
lim<ki⩽logm,可以直接暴力找。
弄完这些后我们可以发现,对于任意的
x
x
x,只有当
x
>
max
i
=
1
k
m
n
i
,
x
%
m
x>\max_{i=1}^kmn_{i,x\%m}
x>maxi=1kmni,x%m
时
F
(
x
)
F(x)
F(x)才为
0
0
0,我们求一下这个最大值构成的区间与
[
l
,
r
]
[l,r]
[l,r]之间的交集中有多少个
%
m
=
x
\% m=x
%m=x的数即可。
时间复杂度 O ( m log m ) O\left(m\log m\right) O(mlogm)差不多吧。
源码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
typedef unsigned int uint;
#define MAXN 1000005
#define MAXM 15
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const LL INF=0x3f3f3f3f3f3f3f3f;
const int mo=998244353;
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int m,p[MAXM],a[MAXM],f[MAXM],cntp,num[MAXN];
LL mn[MAXM][MAXN],l,r,ans;
int main(){
//freopen("sfac.in","r",stdin);
//freopen("sfac.out","w",stdout);
read(l);read(r);read(m);l--;
for(int i=2,t=m;i<=t;i++)if(t%i==0){
++cntp;p[cntp]=i;f[cntp]=1;
while(t%i==0)t/=i,f[cntp]*=i,a[cntp]++;
}
for(int i=1;i<=cntp;i++){
for(int j=0;j<m;j++)num[j]=1,mn[i][j]=-1;
for(int j=0;j<a[i]*p[i];j++){
LL s=1ll*j*j;if(s>=r)break;
for(int k=s%p[i];k<m;k+=p[i])if(num[k]){
num[k]=1ll*(k-s%f[i]+f[i])*num[k]%f[i];
if(!num[k])mn[i][k]=s;
}
}
}
for(int i=0;i<m;i++){
LL maxx=0;bool flag=0;
for(int j=1;j<=cntp;j++)
if(mn[j][i]<0){flag=1;break;}
else maxx=max(mn[j][i],maxx);
if(!flag){
if(maxx<=r)ans+=(r+(m-i)%m)/m-(maxx+(m-i)%m)/m;
if(maxx<=l)ans-=(l+(m-i)%m)/m-(maxx+(m-i)%m)/m;
}
}
printf("%lld\n",ans);
return 0;
}






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








