[航海协会]树

树

题目概述

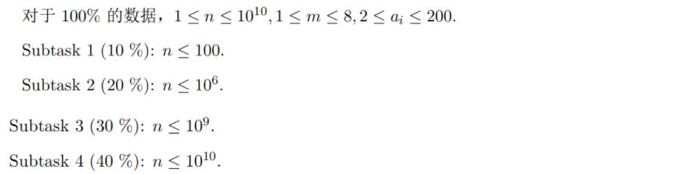
题解

首先看到这道题，一种比较显然的想法是通过生成函数来表我们的方案数。
我们记$f$表示根节点权值为$n$的狄利克雷生成函数，$p=\sum [\exists j,a_j|i]x^i$，也就是叶子上的狄利克雷生成函数，容易得到转移式：
$$f=p+\sum _{i=2}^{\infty }{f}^i=p+\frac{f^2}{1-f}$$答案就是$f$的前$n$项系数和，但看上去这东西不太好解的样子，我们不妨考虑将$f$表示成关于$p$的函数$G(p)$，那么可以得到
$$\begin{gathered} G=p+\frac{G^2}{1-G} \\ 2G^2-(p+1)G+p=0 \\ G=\frac{(p+1)\pm \sqrt{p^2-6p+1}}{4} \end{gathered}$$这样的话，我们就可以考虑通过多项式开根求出我们$G$关于$p$的多项式。
事实上，我们只需要保留$G$中的前${\log }_{\min a}n$次项，再之后的显然前$n$项的和都是$0$了。
这样我们关于$G$的计算就比较简单了，同时也成功地把不同次项的$p^k$独立了出来。
考虑每个$p^k$产生贡献，显然是在$G$中的系数乘上$p^k$里的前缀和。
我们前面是把$p$当成一个自变量来看的，所以前面关于$p^k$系数的计算都是依照普通多项式乘法的方式进行的。
但之后求$p^k$的前$n$项是需要涉及到$p$自己卷上$k$次的$p^k$，这部分采用的实际上都是狄利克雷卷积，考虑怎么对这个式子算前$n$项的和。

显然，一个比较经典的做法是杜教筛。
我们用$p$卷上$p^{k-1}$得到$p^k$的前缀和，有式子：
$$S^k(n)=\sum p(i)S^{k-1}(\lfloor \frac{n}{x}\rfloor )$$显然，后面部分是可以通过数论分块快速计算的。
最开始的$S^1(n)$的每个块位置的前缀和通过容斥就可以$O\left(2^m\sqrt{n}\right)$地算出，之后就在每一层对每个前缀和数论分块计算。
这样的话时间复杂度是$O\left(2^m(\sqrt{n}+m)+n^{\frac{3}{4}}\log n\right)$的，实测会$T$。

没事，杜教筛一个经典的优化方法就是较小部分的前缀和通过筛子预处理出来。
显然，我们这里是不太能线性筛，但仍能做到$O\left(n\ln n\right)$的调和级数复杂度欧拉筛预处理，也就是暴力将$p$和$p^{k-1}$狄利克雷卷积。
于是我们就根号分治一下，小于$B$的部分每层都做一次欧拉筛，大于$B$的部分用我们上面提及的方法杜教筛。
这样就能将时间复杂度做到$O\left(2^m(\sqrt{n}+m)+n^{\frac{2}{3}}{\log }^{\frac{4}{3}}n\right)$，不是严格的，因为约到后面非$0$的部分也就越少了，实测跑得比官方题解做法快。

源码

直接把多项式开根后的结果打下来了（懒

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL,int> pii;
#define MAXN 200005
#define MAXM (1<<8)+5
#define MAXT 3000005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
const int mo=1e9+7;
template<typename _T>
void read(_T &x){
    _T f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
    x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int val[100]={0,1,1,3,11,45,197,903,4279,20793,103049,518859,2646723,13648869,71039373,247693514,468801496,463578229,232754183,380649008,820784009,955296833,998192089,42284528,24749957,215162896,900746364,65025970,285836524,635215250,553669458,753727434,948043668,848863442};
LL n,a[MAXN],d[MAXM];int m,b[15],id1[MAXN],id2[MAXN],pre[MAXT];
int idx,f[40][MAXN],ans,bit[MAXM],sum[MAXN],g[MAXT],t[MAXT];
bool oula[MAXT];
LL getAns(LL x){
    LL res=0;
    for(int i=1;i<(1<<m);i++)
        if(bit[i]&1)res+=x/d[i];else res-=x/d[i];
    return res;
}
int Id(LL x){return n/x<=x?id2[n/x]:id1[x];}
int main(){
    freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout);
    read(n);read(m);for(int i=1;i<=m;i++)read(b[i]);const int n1=min(3000000LL,n);
    for(int i=1;i<(1<<m);i++)bit[i]=bit[i>>1]+(i&1),d[i]=1;
    for(LL l=1,r;l<=n;l=r+1)r=n/(n/l),a[++idx]=n/l;
    for(int i=1;i<=m;i++)for(int j=b[i];j<=n1;j+=b[i])oula[j]=1;
    for(int i=2;i<=n1;i++)g[i]=oula[i],pre[i]=pre[i-1]+oula[i];
    for(int i=1;i<(1<<m);i++)
        for(int j=1;j<=m;j++)if((i>>j-1)&1)
            d[i]=min(1ll*b[j]*d[i]/gcd(d[i],b[j]),n+1);
    sort(a+1,a+idx+1);
    for(int i=1;i<=idx;i++){
        if(n/a[i]<=a[i])id2[n/a[i]]=i;
        else id1[a[i]]=i;
        if(a[i]>n1)f[1][i]=sum[i]=getAns(a[i])%mo;
        else f[1][i]=sum[i]=pre[a[i]];
    }
    ans=f[1][idx];bool flag=0;
    for(int i=2;f[i-1][idx];i++){
        if(!flag){
            for(int j=2;j<=n1/2;j++)if(g[j])
                for(int k=2;k<=n1/j;k++)if(oula[k])
                    Add(t[j*k],g[j],mo);
            for(int j=2;j<=n1;j++)g[j]=t[j],t[j]=0,
                pre[j]=add(pre[j-1],g[j],mo);
            if(!pre[n1])flag=1;else flag=0;
        }
        for(int j=1;j<=idx;j++){
            LL x=a[j];int summ=0;if(x<=n1){f[i][j]=pre[x];continue;}
            for(LL l=1,r,las=0;l<x;l=r+1){
                r=x/(x/l);int tmp=sum[Id(r)],tp=f[i-1][Id(x/r)];
                summ=(1ll*add(tmp,mo-las,mo)*tp+summ)%mo;
                las=tmp;if(!tp)break;
            }
            f[i][j]=summ;
        }
        Add(ans,1ll*val[i]*f[i][idx]%mo,mo);
    }
    printf("%d\n",ans);
    return 0;
}

谢谢！！！