2021-10-22一个数学游戏

问题：

在一次数学游戏中，老师在三个盘子里分别放了一些糖果，糖果数依次为a0,b0,c0，记为（，，）．游戏规则如下：若三个盘子中的糖果数不完全相同，则从糖果数最多的一个盘子中拿出两个，给另外两个盘子各放一个（若有两个盘子中的糖果数相同，且都多于第三个盘子中的糖果数，则从这两个盘子字母序在前的盘子中取糖果），记为一次操作．若三个盘子中的糖果数都相同，游戏结束．次操作后的糖果数记为（，，）．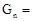
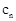（1）若（4，7，10），则第_______次操作后游戏结束；
（2）小明发现：若（4，8，18），则游戏永远无法结束，那么________．

问题分析

通过代码模拟操作

public static void main(String[] args) {
    //int x[] = {4, 7, 10};
    int x[] = {4, 8, 18};
    System.out.println(JsonUtils.toJsonString(fun(x, 0, 2014)));

}

public static int max(int... numberArray) {

    if (ArrayUtil.isEmpty(numberArray)) {
        throw new IllegalArgumentException("Number array must not empty !");
    } else {
        int max = numberArray[0];
        int j = 0;
        for (int i = 1; i < numberArray.length; ++i) {
            if (max < numberArray[i]) {
                max = numberArray[i];
                j = i;
            }
        }

        return j;
    }
}

public static int[] fun(int[] x, int step, int max) {
    if (step == max) {
        if (allEq(x)) {
            System.out.println("suc:" + step);
            return x;
        } else {
            System.out.println("fail:" + step);
            return x;
        }
    }
    while (step < max) {
        if (allEq(x)) {
            System.out.println("suc:" + step);
            return x;
        }
        int index = max(x);
        if (index == 0) {
            x[0] = x[0] - 2;
            x[1] = x[1] + 1;
            x[2] = x[2] + 1;

        } else if (index == 1) {
            x[1] = x[1] - 2;
            x[0] = x[0] + 1;
            x[2] = x[2] + 1;
        } else {
            x[2] = x[2] - 2;
            x[1] = x[1] + 1;
            x[0] = x[0] + 1;
        }
        step++;
        System.out.println("step=" + step+","+JsonUtils.toJsonString(x));
    }
    System.out.println("step=" + step);
    return x;

}

private static boolean allEq(int[] x) {
    return x[0] == x[1] && x[1] == x[2];
}

通过模拟，

step=1,[5,9,16]
step=2,[6,10,14]
step=3,[7,11,12]
step=4,[8,12,10]
step=5,[9,10,11]
step=6,[10,11,9]
step=7,[11,9,10]
step=8,[9,10,11]发现规律，5次操作后3次一循环。

所以，G2014=[11,9,10]

数学推导：

结论：

1）三个数的和如果不能被3整除，那么无法通过若干次操作，变为三数相等；

2）三个数的和如果能被3整除，那么不是所有初始状态通过若干次操作能使得三数相等；

假设第i次操作后的状态为：Gi=(ai,bi,ci)，

三者最大数max(i)=max{ai,bi,ci} ，最小数min(i)=min{ai,bi,ci},

mid(i)为三者的中间数

引理：记d(i)=max(i)-min(i), 那么当d(i)>=3 时，d(i+1)<=d(i) ，等号成立当且仅当mid(i)=max(i)；

证明：因为d(i+1)=max(i+1)-min(i+1），第i+1次操作后的状态:

G(i+1)= (max(i)-2, mid(i)+1,min(i)+1）,

根据，max(i)-min(i)>=3,推出max(i)-2>=min(i)+1, 又因为mid(i)+1>=min(i)+1,所以min(i+1)=min(i)+1,

所以d(i+1)=max(i+1)-min(i)-1；

若max(i+1)=max(i)-2,那么d(i+1)=max(i)-min(i）-3=d（i）-3<d（i）;

若max(i+1)=mid(i)+1，那么，d(i+1)=mid（i)-min(i)<=d（i）, 当max(i)=mid（i) 等号成立

所以d（i）是递减序列，不断减小，

假设第n次变换后，当d（n）<3

若d(n)=0,这种情况三数相同，游戏结束，他三个的和能被3整除；

若d(n)=1, 有2种情况，（a，a，a+1） 和（a，a+1，a+1）这两种情况后面都会以3次操作为循环

若d(n)=2, 有3种情况，（a，a，a+2）， （a，a+1，a+2），（ a，a+2，a+2）这三种，这三个也是会以3次操作为循环，（a，a+1，a+2）比较特殊，他三个的和能被3整除，但是无法变化为三数相同