12.1 常数项级数的概念和性质

 

12.1 常数项级数的概念和性质

第十二章 无穷级数

无穷级数是高等数学的重要组成部分，它是表示函数、研究函数的性质以及进行数值计算的工具。本章先讨论常数项级数，介绍无穷级数的一些基本内容，然后讨论函数项级数，着重讨论如何将函数展开成幂级数和三角级数的问题。

第一节 常数项级数的概念和性质

一、常数项级数的概念

人们在认识事物数量特性时，往往经历一个由近似到精确的过程。在这种认识过程中，会遇到由有限个数量相加到无穷多个数量相加的问题。

例如，计算半径为 RRR 的圆面积 AAA ，具体做法如下：作圆的内接正六边形，算出这个六边形的面积 a1a_1a1​ ，它是圆面积 AAA 的一个粗略的近似值。为了更准确地计算出 AAA 的值，我们以这个正六边形的每一边为底分别作一个顶点在圆周上的等腰三角形（图 12-1），算出这六个等腰三角形的面积之和 a2a_2a2​ 。那么 a1+a2a_1 + a_2a1​+a2​ （即内接正十二边形的面积）就是 AAA 的一个较好的近似值。同样地，在正十二边形的每一边上分别作一个顶点在圆周上的等腰三角形，算出这十二个等腰三角形的面积之和 a3a_3a3​ 。那么 a1+a2+a3a_1 + a_2 + a_3a1​+a2​+a3​ （即内接正二十四边形的面积）是 AAA 的一个更好的近似值。如此继续下去，内接正 3×2n3 \times 2^n3×2n 边形的面积就逐步逼近圆面积：

如果内接正多边形的边数无限增多，即 nnn 无限增大，那么和 a1+a2+⋯+ana_1 + a_2 + \dots + a_na1​+a2​+⋯+an​ 的极限就是所要求的圆面积 AAA 。这时和式中的项数无限增多，于是出现了无穷多个数量依次相加的数学式子。

一般地，如果给定一个数列 u1,u2,u3,…,un,…u_1, u_2, u_3, \dots, u_n, \dotsu1​,u2​,u3​,…,un​,… ，那么由这数列构成的表达式：

即叫做（常数项）无穷级数，简称（常数项）级数，记为：

其中第 nnn 项 unu_nun​ 叫做级数的一般项。

上述级数的定义只是一个形式上的定义，怎样理解无穷级数中无穷多个数量相加呢？联系上面关于计算圆面积的例子，我们可以从有限项的和出发，观察它们的变化趋势，由此来理解无穷多个数量相加的含义。

作（常数项）级数的前 nnn 项的和：

SnS_nSn​ 称为级数的部分和。当 nnn 依次取 1, 2, 3, \dots 时，它们构成一个新的数列：

根据这个数列有没有极限，我们引进无穷级数的收敛与发散的概念。

定义：如果级数的部分和数列 {Sn}\{S_n\}{Sn​} 有极限 SSS ，即：

那么称无穷级数 ∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞​un​ 收敛，这时极限 SSS 叫做这级数的和，并写成：

如果 SnS_nSn​ 没有极限，那么称无穷级数 ∑n=1∞un\sum_{n=1}^{\infty} u_n∑n=1∞​un​ 发散。

显然，当级数收敛时，其部分和 SnS_nSn​ 是级数的和 SSS 的近似值，它们之间的差值：

叫做级数的余项。用近似值 SnS_nSn​ 代替和 SSS 所产生的误差是这个余项的绝对值，即误差是 ∣Rn∣|R_n|∣Rn​∣ 。

从上述定义可知，级数与数列极限有着紧密的联系。给定级数 ∑un\sum u_n∑un​ ，就有部分和数列 {Sn}\{S_n\}{Sn​} ；反之，给定数列 {Sn}\{S_n\}{Sn​} ，就有以 SnS_nSn​ 为部分和数列的级数：

即：

图 12-1

 

例1 无穷级数

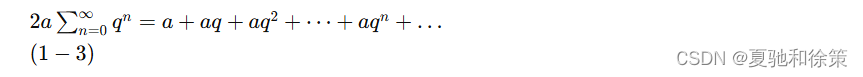
叫做等比级数（又称为几何级数），其中 a≠0a \neq 0a=0， qqq 叫做级数的公比。试讨论级数 (1-3) 的收敛性。

解

如果 q≠1q \neq 1q=1，那么部分和：

如果 ∣q∣=1|q| = 1∣q∣=1，那么当 q=1q = 1q=1 时，Sn=a(n+1)→∞S_n = a(n+1) \to \inftySn​=a(n+1)→∞，因此级数 (1-3) 发散；当 q=−1q = -1q=−1 时，级数 (1-3) 成为：

显然 SnS_nSn​ 随着 nnn 为奇数或为偶数而等于 aaa 或等于 0，从而 SnS_nSn​ 的极限不存在，这时级数 (1-3) 也发散。

综合上述结果，我们得到：如果等比级数 (1-3) 的公比的绝对值 ∣q∣<1|q| < 1∣q∣<1，那么级数收敛；如果 ∣q∣≥1|q| \ge 1∣q∣≥1，那么级数发散。

证

这级数的部分和为：

显然，lim⁡n→∞Sn=∞\lim_{n \to \infty} S_n = \inftylimn→∞​Sn​=∞，因此所给级数是发散的。

解

由于：

因此：

从而：

所以这级数收敛，它的和是 2。

 

 

二、收敛级数的基本性质

根据无穷级数的收敛、发散以及和的概念，可以得出收敛级数的几个基本性质。

性质1：常数倍级数

如果级数 ∑un\sum u_n∑un​ 收敛于和 SSS，那么级数 ∑kun\sum k u_n∑kun​ 也收敛，且其和为 kSkSkS。

证：设级数 ∑un\sum u_n∑un​ 的部分和分别为 SnS_nSn​，则有：

于是：

这表明级数 ∑kun\sum k u_n∑kun​ 收敛，且和为 kSkSkS。由关系式 σn=kSn\sigma_n = kS_nσn​=kSn​ 知道，如果 SnS_nSn​ 没有极限且 k≠0k \neq 0k=0，那么 σn\sigma_nσn​ 也不可能有极限。因此我们得到如下结论：级数的每一项同乘一个不为零的常数后，它的收敛性不会改变。

性质2：级数相加或相减

如果级数 ∑un\sum u_n∑un​ 与 ∑vn\sum v_n∑vn​ 分别收敛于和 SSS 与 TTT，那么级数 ∑(un±vn)\sum (u_n \pm v_n)∑(un​±vn​) 也收敛，且其和为 S±TS \pm TS±T。

证：设级数 ∑un\sum u_n∑un​ 和 ∑vn\sum v_n∑vn​ 的部分和分别为 SnS_nSn​ 与 TnT_nTn​，则级数 ∑(un±vn)\sum (u_n \pm v_n)∑(un​±vn​) 的部分和为：

这表明级数 ∑(un±vn)\sum (u_n \pm v_n)∑(un​±vn​) 收敛，且其和为 S±TS \pm TS±T。性质2也可以表述为：两个收敛级数可以逐项相加与逐项相减。

性质3：有限项的加减

在级数中去掉、加上或改变有限项，不会改变级数的收敛性。

证：我们只需证明“在级数的前面部分去掉或加上有限项，不会改变级数的收敛性”，因为其他情形（即在级数中任意去掉、加上或改变有限项的情形）都可以看成在级数的前面部分先去掉有限项，然后再加上有限项的结果。

设将级数：

的前 kkk 项去掉，则得级数：

于是新得的级数的部分和为：

其中 Sk+nS_{k+n}Sk+n​ 是原来级数的前 k+nk+nk+n 项的和。因为 SkS_kSk​ 是常数，所以当 n→∞n \to \inftyn→∞ 时，σn\sigma_nσn​ 与 Sk+nS_{k+n}Sk+n​ 或者同时具有极限，或者同时没有极限。

类似地，可以证明在级数的前面加上有限项，不会改变级数的收敛性。

性质4：加括号后的收敛性

如果级数 ∑un\sum u_n∑un​ 收敛，那么对这级数的项任意加括号后所成的级数：

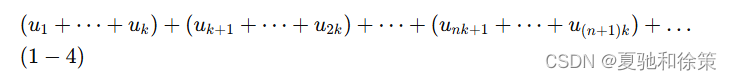
仍收敛，且其和不变。

证：设级数 ∑un\sum u_n∑un​ 的部分和数列为 {Sn}\{ S_n \}{Sn​}，加括号后所成的级数 (1-4) 的部分和数列为 {Am}\{ A_m \}{Am​}，则：

可见，数列 {Am}\{ A_m \}{Am​} 是数列 {Sn}\{ S_n \}{Sn​} 的一个子数列。由数列 {Sn}\{ S_n \}{Sn​} 的收敛性以及收敛数列与其子数列的关系可知，数列 {Am}\{ A_m \}{Am​} 必定收敛，且有：

即加括号后所成的级数收敛，且其和不变。

注意：如果加括号后所成的级数收敛，那么不能断定去括号后原来的级数也收敛。例如，级数：

收敛于零，但级数：

却是发散的。

根据性质4可得如下推论：如果加括号后所成的级数发散，那么原来级数也发散。事实上，倘若原来级数收敛，则根据性质4知道，加括号后的级数就应该收敛了。

性质5：级数收敛的必要条件

如果级数 ∑un\sum u_n∑un​ 收敛，那么它的一般项 unu_nun​ 趋于零，即：

证：设级数 ∑un\sum u_n∑un​ 的部分和为 SnS_nSn​，且 Sn→SS_n \to SSn​→S (当 n→∞n \to \inftyn→∞ )，则：

由性质5可知，如果级数的一般项不趋于零，那么该级数必定发散。例如，级数：

它的一般项 un=(−1)n+1nu_n = (-1)^{n+1} nun​=(−1)n+1n 当 n→∞n \to \inftyn→∞ 时不趋于零，因此该级数是发散的。

注意：级数的一般项趋于零并不是级数收敛的充分条件。有些级数虽然一般项趋于零，但仍然是发散的。例如，调和级数：

虽然它的一般项 1n→0\frac{1}{n} \to 0n1​→0 (当 n→∞n \to \inftyn→∞ )，但是它是发散的。现在我们用反证法证明如下：

假若级数 (1-5) 收敛，设它的部分和为 SnS_nSn​，且 Sn→SS_n \to SSn​→S (当 n→∞n \to \inftyn→∞ )。显然，对级数：

的部分和 Sn−1S_{n-1}Sn−1​，也有 Sn−1→SS_{n-1} \to SSn−1​→S (当 n→∞n \to \inftyn→∞ )。于是：

但另一方面：

故：

与假设级数 (1-5) 收敛矛盾。这矛盾说明级数 (1-5) 必定发散。

 

三、柯西审敛原理

怎样判定一个级数的收敛性呢？我们有下述的柯西审敛原理。

定理（柯西审敛原理）

级数 ∑un\sum u_n∑un​ 收敛的充分必要条件是：对于任意给定的正数 ϵ\epsilonϵ，总存在正整数 NNN，使得当 n>Nn > Nn>N 时，对于任意的正整数 ppp，都有

成立。

证明

设级数 ∑un\sum u_n∑un​ 的部分和为 SnS_nSn​，因为

所以由数列的柯西极限存在准则（第一章第六节），即得本定理结论。

例4 利用柯西审敛原理判定级数的收敛性

利用柯西审敛原理判定以下级数的收敛性。

解

因为

所以部分和为：

因此，

对任何正整数 ppp，

对于任意给定的正数 ϵ\epsilonϵ，取正整数 NNN 使得 1N+1<ϵ\frac{1}{N+1} < \epsilonN+11​<ϵ，则当 n>Nn > Nn>N 时，对任何正整数 ppp，都有：

总结

柯西审敛原理为判定级数收敛提供了一个重要的工具，通过验证部分和之间的差值是否可以任意小，我们可以确定级数的收敛性。例子中的应用展示了如何利用这个原理来具体判定一个级数的收敛性。